Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 201004 by Mingma last updated on 27/Nov/23

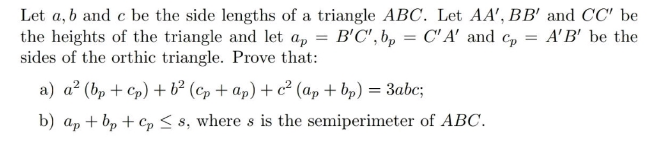
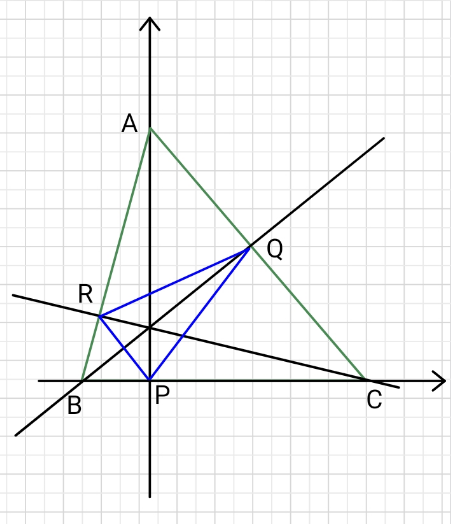
Answered by ajfour last updated on 27/Nov/23

Commented by Mingma last updated on 27/Nov/23

Very elegant, sir!

Answered by ajfour last updated on 28/Nov/23

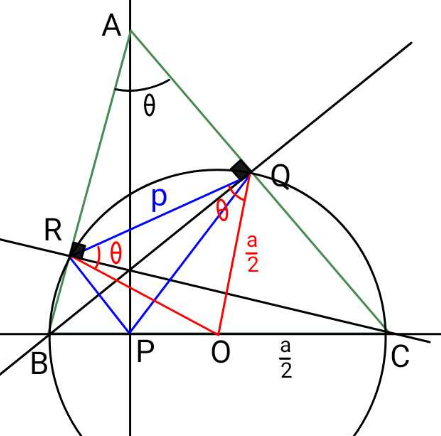
Commented by ajfour last updated on 02/Dec/23

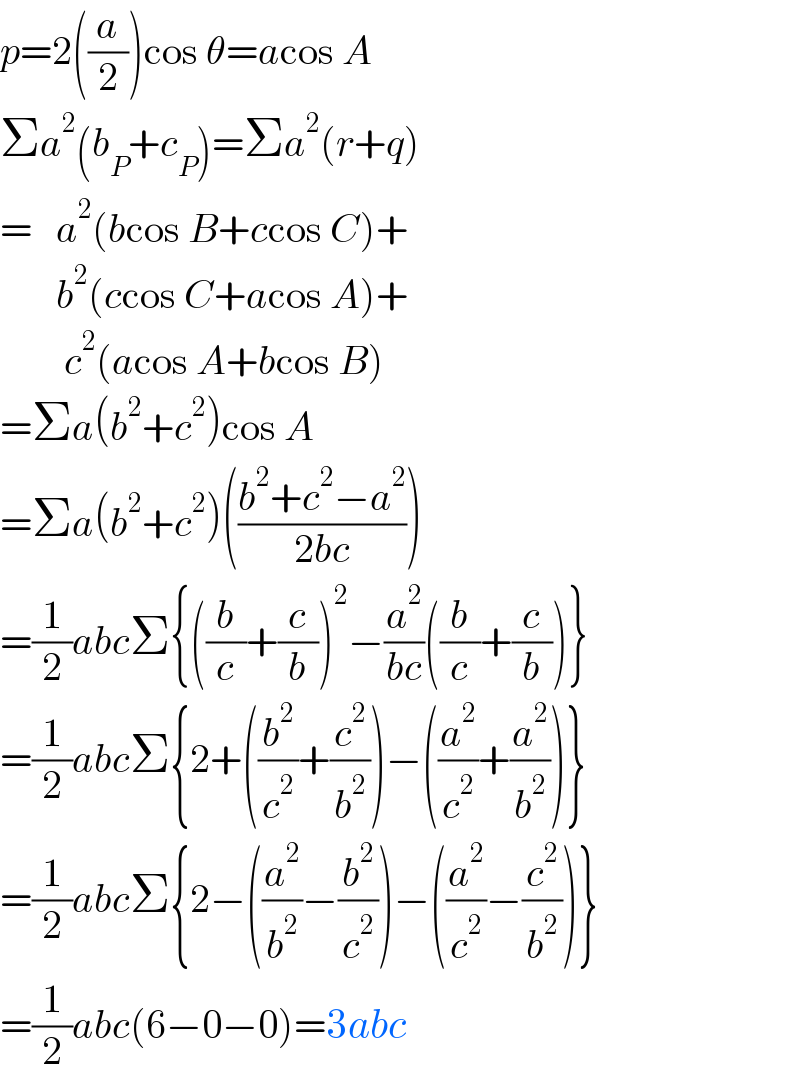
p=2((a/2))cos θ=acos A Σa^2 (b_P +c_P )=Σa^2 (r+q) = a^2 (bcos B+ccos C)+ b^2 (ccos C+acos A)+ c^2 (acos A+bcos B) =Σa(b^2 +c^2 )cos A =Σa(b^2 +c^2 )(((b^2 +c^2 −a^2 )/(2bc))) =(1/2)abcΣ{((b/c)+(c/b))^2 −(a^2 /(bc))((b/c)+(c/b))} =(1/2)abcΣ{2+((b^2 /c^2 )+(c^2 /b^2 ))−((a^2 /c^2 )+(a^2 /b^2 ))} =(1/2)abcΣ{2−((a^2 /b^2 )−(b^2 /c^2 ))−((a^2 /c^2 )−(c^2 /b^2 ))} =(1/2)abc(6−0−0)=3abc

$${p}=\mathrm{2}\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{cos}\:\theta={a}\mathrm{cos}\:{A} \\ $$$$\Sigma{a}^{\mathrm{2}} \left({b}_{{P}} +{c}_{{P}} \right)=\Sigma{a}^{\mathrm{2}} \left({r}+{q}\right) \\ $$$$=\:\:\:{a}^{\mathrm{2}} \left({b}\mathrm{cos}\:{B}+{c}\mathrm{cos}\:{C}\right)+ \\ $$$$\:\:\:\:\:\:\:{b}^{\mathrm{2}} \left({c}\mathrm{cos}\:{C}+{a}\mathrm{cos}\:{A}\right)+ \\ $$$$\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} \left({a}\mathrm{cos}\:{A}+{b}\mathrm{cos}\:{B}\right) \\ $$$$=\Sigma{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\mathrm{cos}\:{A} \\ $$$$=\Sigma{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left(\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{abc}\Sigma\left\{\left(\frac{{b}}{{c}}+\frac{{c}}{{b}}\right)^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{{bc}}\left(\frac{{b}}{{c}}+\frac{{c}}{{b}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{abc}\Sigma\left\{\mathrm{2}+\left(\frac{{b}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{c}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)−\left(\frac{{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{abc}\Sigma\left\{\mathrm{2}−\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{{b}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)−\left(\frac{{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} }−\frac{{c}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{abc}\left(\mathrm{6}−\mathrm{0}−\mathrm{0}\right)=\mathrm{3}{abc} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com