Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 200978 by sonukgindia last updated on 27/Nov/23

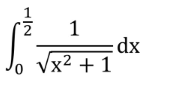
Answered by BaliramKumar last updated on 27/Nov/23

put x = tanθ ⇒ dx = sec^2 θdθ ∫ (1/( (√(tan^2 θ+1))))sec^2 θdθ ∫ secθdθ = ln(secθ + tanθ) ⇒ ln((√(tan^2 θ+1)) + tanθ) ⇒ [ ln((√(x^2 +1)) + x)]_0 ^(1/2) = ln(((1+(√5))/2)) = 0.4812

$$\mathrm{put}\:\:\:\mathrm{x}\:=\:\mathrm{tan}\theta\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\mathrm{dx}\:=\:\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}}}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\int\:\mathrm{sec}\theta\mathrm{d}\theta\:=\:\mathrm{ln}\left(\mathrm{sec}\theta\:+\:\mathrm{tan}\theta\right) \\ $$$$\Rightarrow\:\:\mathrm{ln}\left(\sqrt{\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}}\:+\:\mathrm{tan}\theta\right) \\ $$$$\Rightarrow\:\left[\:\mathrm{ln}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:+\:\mathrm{x}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\mathrm{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:=\:\mathrm{0}.\mathrm{4812} \\ $$$$ \\ $$$$ \\ $$

Answered by MM42 last updated on 27/Nov/23

I=ln(x+(√(1+x^2 )))]_0 ^(1/2) =ln(((1+(√5))/2) ) ✓

$$\left.{I}={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} ={ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\right)\:\:\checkmark \\ $$$$ \\ $$

Answered by Calculusboy last updated on 28/Nov/23

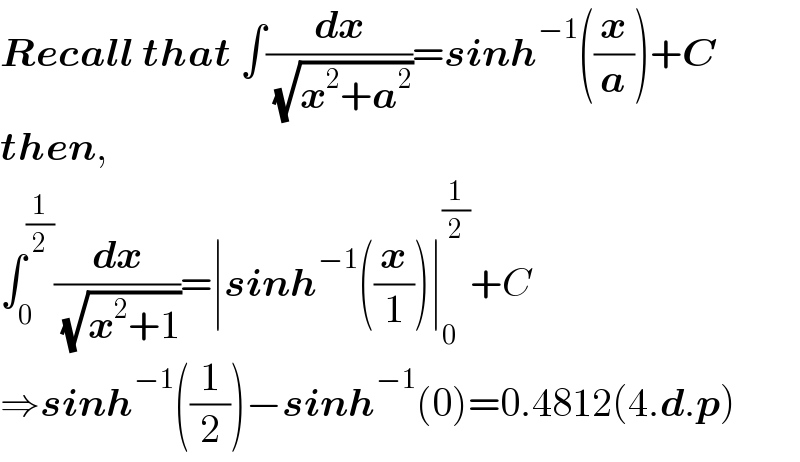
Recall that ∫(dx/( (√(x^2 +a^2 ))))=sinh^(−1) ((x/a))+C then, ∫_0 ^(1/2) (dx/( (√(x^2 +1))))=∣sinh^(−1) ((x/1))∣_0 ^(1/2) +C ⇒sinh^(−1) ((1/2))−sinh^(−1) (0)=0.4812(4.d.p)

$$\boldsymbol{{Recall}}\:\boldsymbol{{that}}\:\int\frac{\boldsymbol{{dx}}}{\:\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{a}}^{\mathrm{2}} }}=\boldsymbol{{sinh}}^{−\mathrm{1}} \left(\frac{\boldsymbol{{x}}}{\boldsymbol{{a}}}\right)+\boldsymbol{{C}} \\ $$$$\boldsymbol{{then}},\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\boldsymbol{{dx}}}{\:\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}=\mid\boldsymbol{{sinh}}^{−\mathrm{1}} \left(\frac{\boldsymbol{{x}}}{\mathrm{1}}\right)\mid_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} +{C} \\ $$$$\Rightarrow\boldsymbol{{sinh}}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\boldsymbol{{sinh}}^{−\mathrm{1}} \left(\mathrm{0}\right)=\mathrm{0}.\mathrm{4812}\left(\mathrm{4}.\boldsymbol{{d}}.\boldsymbol{{p}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com