
Previous in Differential Equation Next in Differential Equation
Question Number 200902 by Rupesh123 last updated on 26/Nov/23
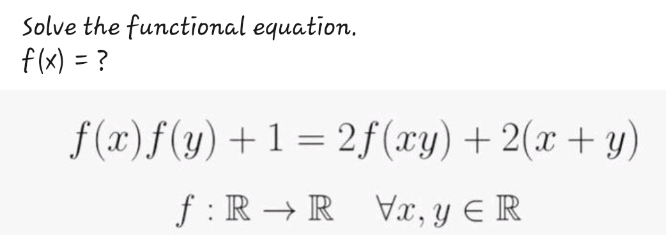
Answered by Rasheed.Sindhi last updated on 26/Nov/23
![f(x)f(y)+1=2f(xy)+2(x+y) x=y=1: [f(1)]^2 +1=2f(1)+4 [f(1)]^2 −2f(1)−3=0 ( f(1)−3 )(f(1)+1 )=0 f(1)=3,−1 y=1: f(x)f(1)+1=2f(x)+2x+2 { ((f(1)=3: 3f(x)−2f(x)=2x+1)),((f(1)=−1: −f(x)−2f(x)=2x+1)) :} ⇒ { ((f(x)=2x+1)),((f(x)=−((2x+1)/3))) :}](Q200905.png)
$${f}\left({x}\right){f}\left({y}\right)+\mathrm{1}=\mathrm{2}{f}\left({xy}\right)+\mathrm{2}\left({x}+{y}\right) \\ $$$${x}={y}=\mathrm{1}: \\ $$$$\left[{f}\left(\mathrm{1}\right)\right]^{\mathrm{2}} +\mathrm{1}=\mathrm{2}{f}\left(\mathrm{1}\right)+\mathrm{4} \\ $$$$\left[{f}\left(\mathrm{1}\right)\right]^{\mathrm{2}} −\mathrm{2}{f}\left(\mathrm{1}\right)−\mathrm{3}=\mathrm{0} \\ $$$$\left(\:{f}\left(\mathrm{1}\right)−\mathrm{3}\:\right)\left({f}\left(\mathrm{1}\right)+\mathrm{1}\:\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{3},−\mathrm{1} \\ $$$${y}=\mathrm{1}: \\ $$$${f}\left({x}\right){f}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{2}{f}\left({x}\right)+\mathrm{2}{x}+\mathrm{2} \\ $$$$\begin{cases}{{f}\left(\mathrm{1}\right)=\mathrm{3}:\:\:\:\:\:\:\mathrm{3}{f}\left({x}\right)−\mathrm{2}{f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1}}\\{{f}\left(\mathrm{1}\right)=−\mathrm{1}:\:\:−{f}\left({x}\right)−\mathrm{2}{f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1}}\end{cases}\:\: \\ $$$$\Rightarrow\begin{cases}{{f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1}}\\{{f}\left({x}\right)=−\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{3}}}\end{cases}\:\: \\ $$
Commented by Rupesh123 last updated on 26/Nov/23
Perfect ��
Commented by deleteduser1 last updated on 26/Nov/23
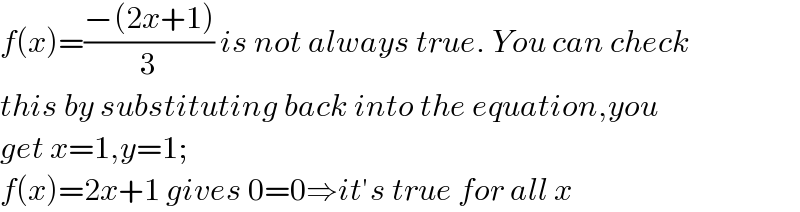
$${f}\left({x}\right)=\frac{−\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:{is}\:{not}\:{always}\:{true}.\:{You}\:{can}\:{check} \\ $$$${this}\:{by}\:{substituting}\:{back}\:{into}\:{the}\:{equation},{you} \\ $$$${get}\:{x}=\mathrm{1},{y}=\mathrm{1};\: \\ $$$${f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1}\:{gives}\:\mathrm{0}=\mathrm{0}\Rightarrow{it}'{s}\:{true}\:{for}\:{all}\:{x} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Nov/23
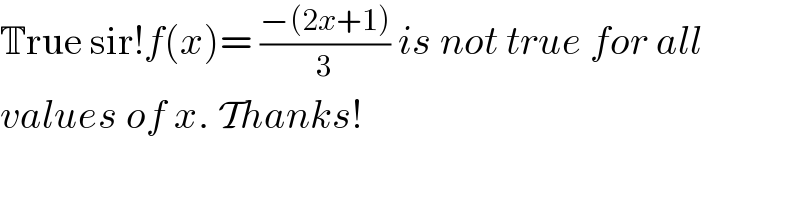
$$\mathbb{T}\mathrm{rue}\:\mathrm{sir}!{f}\left({x}\right)=\:\frac{−\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:{is}\:{not}\:{true}\:{for}\:{all} \\ $$$${values}\:{of}\:{x}.\:\mathcal{T}{hanks}! \\ $$
Answered by deleteduser1 last updated on 26/Nov/23
![[f(0)]^2 −2f(0)+1=0⇒f(0)=1 f(x)f(0)=2f(0)+2x−1⇒f(x)=2x+1](Q200910.png)
$$\left[{f}\left(\mathrm{0}\right)\right]^{\mathrm{2}} −\mathrm{2}{f}\left(\mathrm{0}\right)+\mathrm{1}=\mathrm{0}\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${f}\left({x}\right){f}\left(\mathrm{0}\right)=\mathrm{2}{f}\left(\mathrm{0}\right)+\mathrm{2}{x}−\mathrm{1}\Rightarrow{f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1} \\ $$
Commented by Rupesh123 last updated on 26/Nov/23
Nice!
