
Question Number 200877 by mathlove last updated on 25/Nov/23
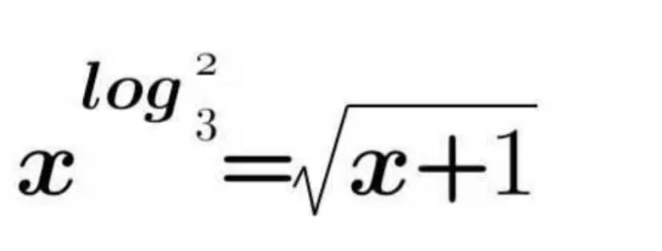
Commented by mr W last updated on 25/Nov/23
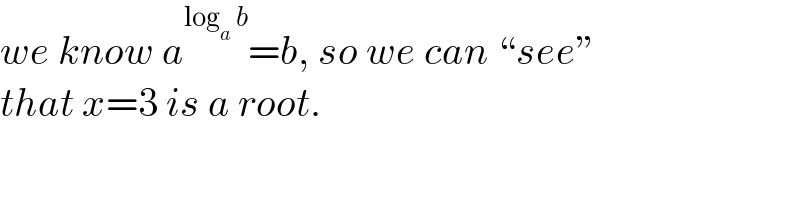
$${we}\:{know}\:{a}^{\mathrm{log}_{{a}} \:{b}} ={b},\:{so}\:{we}\:{can}\:``{see}'' \\ $$$${that}\:{x}=\mathrm{3}\:{is}\:{a}\:{root}. \\ $$
Commented by mathlove last updated on 25/Nov/23

$${thanks} \\ $$
Commented by mathlove last updated on 26/Nov/23
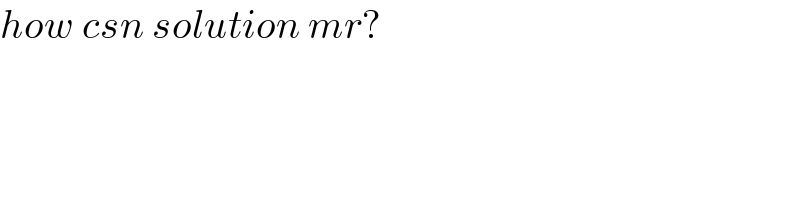
$${how}\:{csn}\:{solution}\:{mr}? \\ $$
Commented by mr W last updated on 26/Nov/23

$${if}\:{it}\:{is}\:{not}\:{obvious}\:{to}\:{you},\:{i}.{e}.\:{if}\:{you} \\ $$$${can}\:{not}\:``{see}''\:{the}\:{solution},\:{then}\:{you} \\ $$$${can}\:{not}\:{solve}\:{it}\:{at}\:{all}.\:{there}\:{is}\:{no} \\ $$$${general}\:{method}\:{to}\:{solve}\:{such}\:{an} \\ $$$${equation}.\:{for}\:{example}\:{the}\:{root}\:{from} \\ $$$$\:{x}^{\mathrm{log}_{\mathrm{2}} \:\mathrm{3}} =\sqrt{{x}+\mathrm{1}}\:{is}\:{not}\:{obvious},\:{so}\:{you} \\ $$$${can}\:{not}\:{solve}\:{it}\:\left({exactly}\right). \\ $$
Commented by mathlove last updated on 26/Nov/23

$${ok}\:{thanks} \\ $$
