
Question Number 200816 by mr W last updated on 23/Nov/23
Commented by mr W last updated on 23/Nov/23
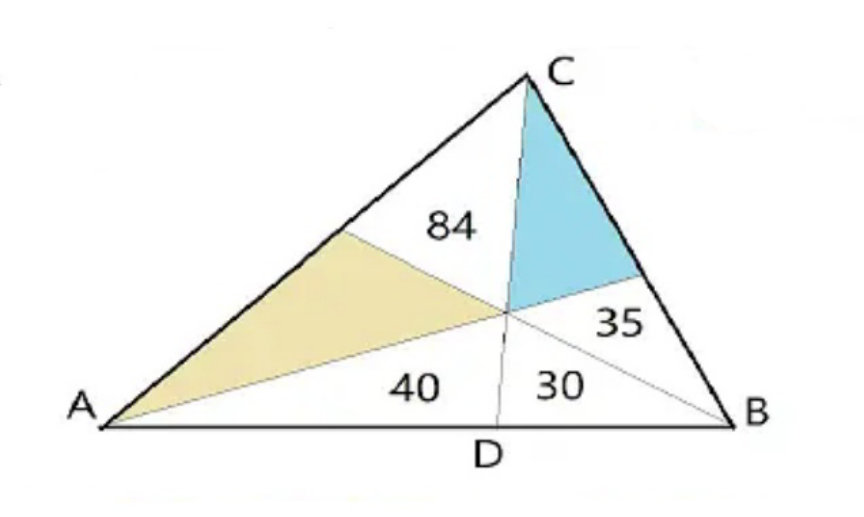
$${find}\:{the}\:{colored}\:{areas}. \\ $$
Commented by Ari last updated on 24/Nov/23
$${excuse}\:{me}\:{are}\:{the}\:{segment}\:{from}\:{vertices} \\ $$$${half}\:{of}\:{the}\:{angles}? \\ $$
Commented by mr W last updated on 24/Nov/23

$${not}\:{sure}.\:{only}\:{the}\:{areas}\:{are}\:{given}. \\ $$
Answered by deleteduser1 last updated on 24/Nov/23
![((AD)/(DB))=(([AGD])/([GDB]))=(4/3);Let [CGF]=r ∧[GEA]=s ((84)/s)×(4/3)×((35)/r)=1⇒rs=3920 (([AFC])/([ABF]))=((84+r+s)/(105))=(r/(35))⇒2r=84+((3920)/r) ⇒2r^2 −84r−3920=0⇒r=70⇒s=56](Q200819.png)
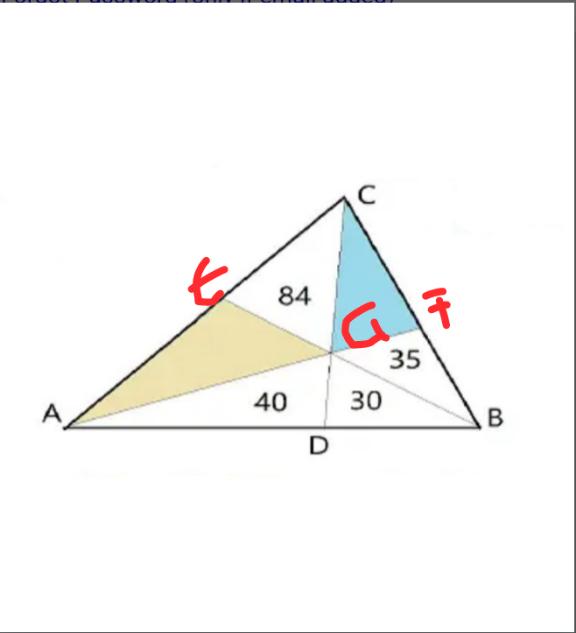
$$\frac{{AD}}{{DB}}=\frac{\left[{AGD}\right]}{\left[{GDB}\right]}=\frac{\mathrm{4}}{\mathrm{3}};{Let}\:\left[{CGF}\right]={r}\:\wedge\left[{GEA}\right]={s} \\ $$$$\frac{\mathrm{84}}{{s}}×\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{35}}{{r}}=\mathrm{1}\Rightarrow{rs}=\mathrm{3920} \\ $$$$\frac{\left[{AFC}\right]}{\left[{ABF}\right]}=\frac{\mathrm{84}+{r}+{s}}{\mathrm{105}}=\frac{{r}}{\mathrm{35}}\Rightarrow\mathrm{2}{r}=\mathrm{84}+\frac{\mathrm{3920}}{{r}} \\ $$$$\Rightarrow\mathrm{2}{r}^{\mathrm{2}} −\mathrm{84}{r}−\mathrm{3920}=\mathrm{0}\Rightarrow{r}=\mathrm{70}\Rightarrow{s}=\mathrm{56} \\ $$
Commented by deleteduser1 last updated on 24/Nov/23
Commented by mr W last updated on 24/Nov/23

$${yes}.\:{thanks}! \\ $$
Answered by mr W last updated on 24/Nov/23

$$\frac{\mathrm{84}+{y}}{\mathrm{40}}=\frac{{b}+\mathrm{35}}{\mathrm{30}} \\ $$$$\Rightarrow\mathrm{3}{y}−\mathrm{4}{b}=−\mathrm{112}\:\:\:...\left({i}\right) \\ $$$$\frac{\mathrm{40}+\mathrm{30}}{\mathrm{35}}=\frac{\mathrm{84}+{y}}{{b}} \\ $$$$\Rightarrow{y}−\mathrm{2}{b}=−\mathrm{84}\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{y}=\mathrm{56}={yellow}\:{area} \\ $$$$\Rightarrow{b}=\mathrm{70}={blue}\:{area} \\ $$
