Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 200570 by Rupesh123 last updated on 20/Nov/23

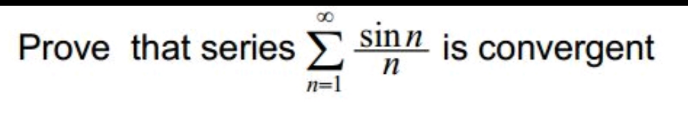
Answered by witcher3 last updated on 20/Nov/23

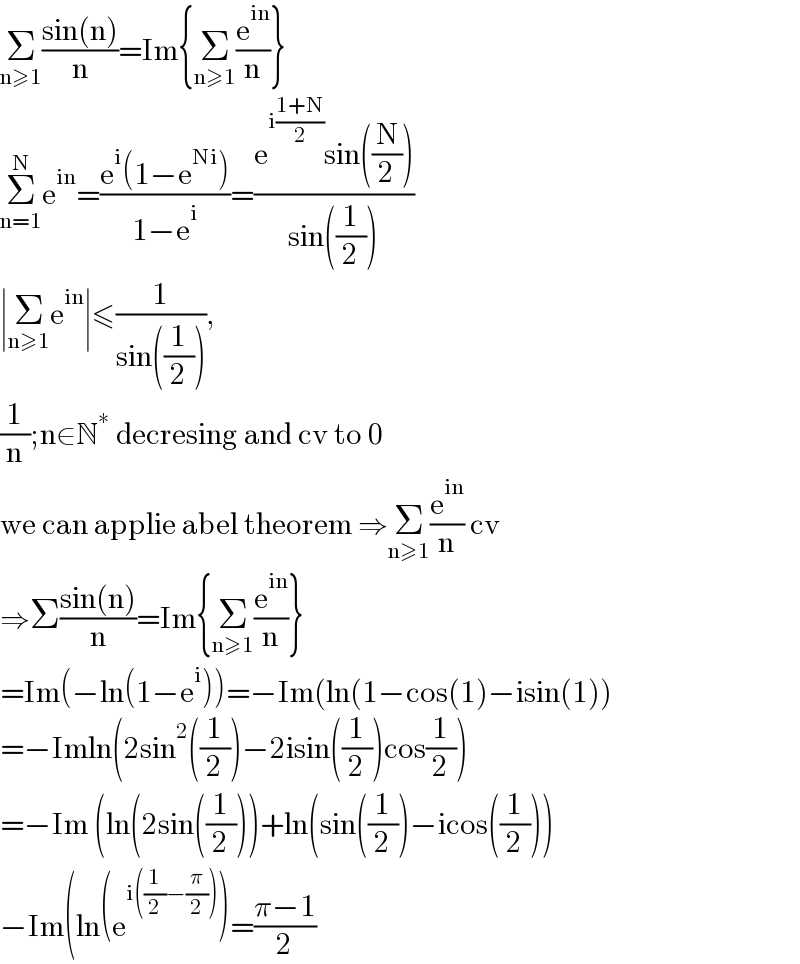
Σ_(n≥1) ((sin(n))/n)=Im{Σ_(n≥1) (e^(in) /n)} Σ_(n=1) ^N e^(in) =((e^i (1−e^(Ni) ))/(1−e^i ))=((e^(i((1+N)/2)) sin((N/2)))/(sin((1/2)))) ∣Σ_(n≥1) e^(in) ∣≤(1/(sin((1/2)))), (1/n);n∈N^∗ decresing and cv to 0 we can applie abel theorem ⇒Σ_(n≥1) (e^(in) /n) cv ⇒Σ((sin(n))/n)=Im{Σ_(n≥1) (e^(in) /n)} =Im(−ln(1−e^i ))=−Im(ln(1−cos(1)−isin(1)) =−Imln(2sin^2 ((1/2))−2isin((1/2))cos(1/2)) =−Im (ln(2sin((1/2)))+ln(sin((1/2))−icos((1/2))) −Im(ln(e^(i((1/2)−(π/2))) )=((π−1)/2)

$$\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}}=\mathrm{Im}\left\{\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{e}^{\mathrm{in}} }{\mathrm{n}}\right\} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\mathrm{e}^{\mathrm{in}} =\frac{\mathrm{e}^{\mathrm{i}} \left(\mathrm{1}−\mathrm{e}^{\mathrm{Ni}} \right)}{\mathrm{1}−\mathrm{e}^{\mathrm{i}} }=\frac{\mathrm{e}^{\mathrm{i}\frac{\mathrm{1}+\mathrm{N}}{\mathrm{2}}} \mathrm{sin}\left(\frac{\mathrm{N}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\mid\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{e}^{\mathrm{in}} \mid\leqslant\frac{\mathrm{1}}{\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)},\: \\ $$$$\frac{\mathrm{1}}{\mathrm{n}};\mathrm{n}\in\mathbb{N}^{\ast} \:\mathrm{decresing}\:\mathrm{and}\:\mathrm{cv}\:\mathrm{to}\:\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{applie}\:\mathrm{abel}\:\mathrm{theorem}\:\Rightarrow\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{e}^{\mathrm{in}} }{\mathrm{n}}\:\mathrm{cv} \\ $$$$\Rightarrow\Sigma\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}}=\mathrm{Im}\left\{\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{e}^{\mathrm{in}} }{\mathrm{n}}\right\} \\ $$$$=\mathrm{Im}\left(−\mathrm{ln}\left(\mathrm{1}−\mathrm{e}^{\mathrm{i}} \right)\right)=−\mathrm{Im}\left(\mathrm{ln}\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{1}\right)−\mathrm{isin}\left(\mathrm{1}\right)\right)\right. \\ $$$$=−\mathrm{Imln}\left(\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{cos}\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=−\mathrm{Im}\:\left(\mathrm{ln}\left(\mathrm{2sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+\mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{icos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\right. \\ $$$$−\mathrm{Im}\left(\mathrm{ln}\left(\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\right)} \right)=\frac{\pi−\mathrm{1}}{\mathrm{2}}\right. \\ $$

Commented by Rupesh123 last updated on 20/Nov/23

Nice one!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com