
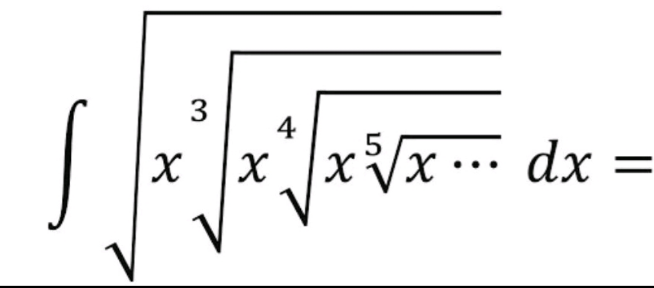
Question Number 200569 by Rupesh123 last updated on 20/Nov/23
Answered by MM42 last updated on 20/Nov/23
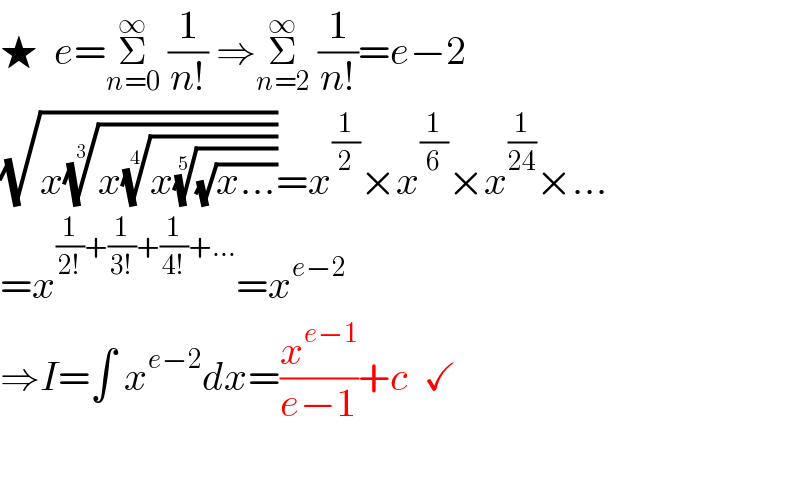
$$\bigstar\:\:{e}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}!}\:\Rightarrow\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}!}={e}−\mathrm{2} \\ $$$$\sqrt{{x}\sqrt[{\mathrm{3}}]{{x}\sqrt[{\mathrm{4}}]{{x}\sqrt[{\mathrm{5}}]{\sqrt{{x}...}}}}}={x}^{\frac{\mathrm{1}}{\mathrm{2}}} ×{x}^{\frac{\mathrm{1}}{\mathrm{6}}} ×{x}^{\frac{\mathrm{1}}{\mathrm{24}}} ×... \\ $$$$={x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+...} ={x}^{{e}−\mathrm{2}} \\ $$$$\Rightarrow{I}=\int\:{x}^{{e}−\mathrm{2}} {dx}=\frac{{x}^{{e}−\mathrm{1}} }{{e}−\mathrm{1}}+{c}\:\:\checkmark \\ $$$$ \\ $$
Commented by Rupesh123 last updated on 20/Nov/23
Nice one, sir!
Commented by MM42 last updated on 20/Nov/23

$$\:\underline{\underbrace{\lesseqgtr}} \\ $$
Commented by Harnada last updated on 21/Nov/23

$${Q}.\mathrm{1}\: \\ $$
