
Question Number 200476 by Rupesh123 last updated on 19/Nov/23

Answered by deleteduser1 last updated on 19/Nov/23
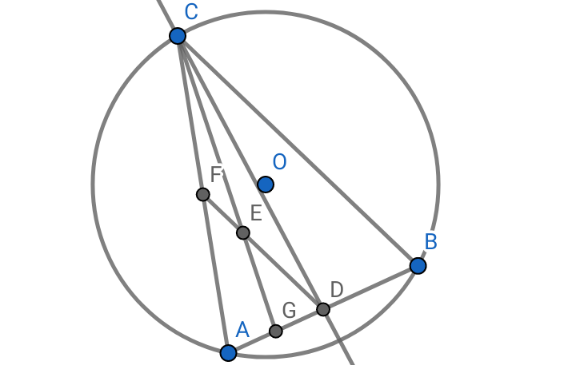
Commented by deleteduser1 last updated on 19/Nov/23
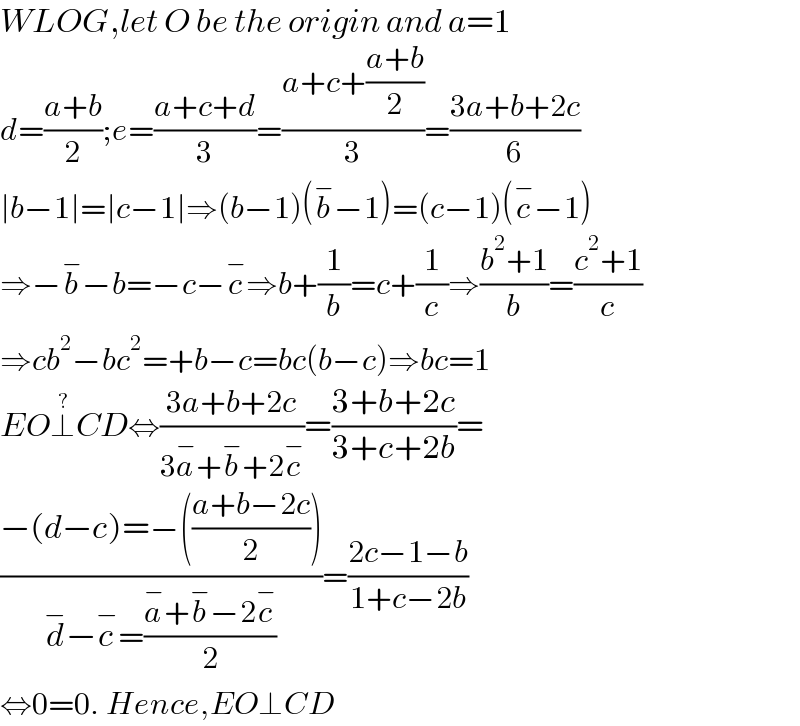
$${WLOG},{let}\:{O}\:{be}\:{the}\:{origin}\:{and}\:{a}=\mathrm{1}\: \\ $$$${d}=\frac{{a}+{b}}{\mathrm{2}};{e}=\frac{{a}+{c}+{d}}{\mathrm{3}}=\frac{{a}+{c}+\frac{{a}+{b}}{\mathrm{2}}}{\mathrm{3}}=\frac{\mathrm{3}{a}+{b}+\mathrm{2}{c}}{\mathrm{6}} \\ $$$$\mid{b}−\mathrm{1}\mid=\mid{c}−\mathrm{1}\mid\Rightarrow\left({b}−\mathrm{1}\right)\left(\overset{−} {{b}}−\mathrm{1}\right)=\left({c}−\mathrm{1}\right)\left(\overset{−} {{c}}−\mathrm{1}\right) \\ $$$$\Rightarrow−\overset{−} {{b}}−{b}=−{c}−\overset{−} {{c}}\Rightarrow{b}+\frac{\mathrm{1}}{{b}}={c}+\frac{\mathrm{1}}{{c}}\Rightarrow\frac{{b}^{\mathrm{2}} +\mathrm{1}}{{b}}=\frac{{c}^{\mathrm{2}} +\mathrm{1}}{{c}} \\ $$$$\Rightarrow{cb}^{\mathrm{2}} −{bc}^{\mathrm{2}} =+{b}−{c}={bc}\left({b}−{c}\right)\Rightarrow{bc}=\mathrm{1} \\ $$$${EO}\overset{?} {\bot}{CD}\Leftrightarrow\frac{\mathrm{3}{a}+{b}+\mathrm{2}{c}}{\mathrm{3}\overset{−} {{a}}+\overset{−} {{b}}+\mathrm{2}\overset{−} {{c}}}=\frac{\mathrm{3}+{b}+\mathrm{2}{c}}{\mathrm{3}+{c}+\mathrm{2}{b}}= \\ $$$$\frac{−\left({d}−{c}\right)=−\left(\frac{{a}+{b}−\mathrm{2}{c}}{\mathrm{2}}\right)}{\overset{−} {{d}}−\overset{−} {{c}}=\frac{\overset{−} {{a}}+\overset{−} {{b}}−\mathrm{2}\overset{−} {{c}}}{\mathrm{2}}}=\frac{\mathrm{2}{c}−\mathrm{1}−{b}}{\mathrm{1}+{c}−\mathrm{2}{b}} \\ $$$$\Leftrightarrow\mathrm{0}=\mathrm{0}.\:{Hence},{EO}\bot{CD} \\ $$
Commented by Rupesh123 last updated on 20/Nov/23
Very elegant, sir!
