Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 200379 by cortano12 last updated on 18/Nov/23

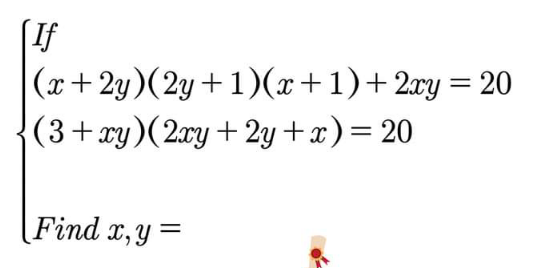
Commented by Frix last updated on 18/Nov/23

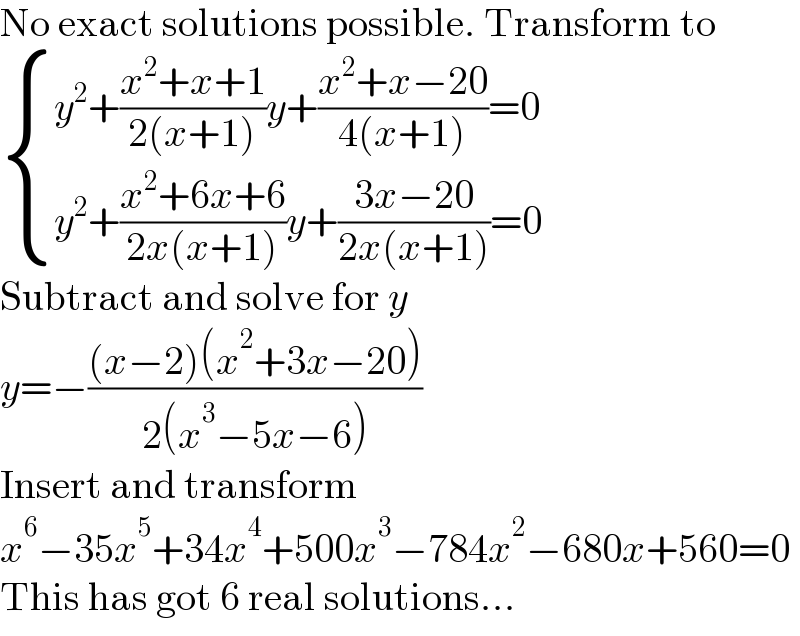
No exact solutions possible. Transform to { ((y^2 +((x^2 +x+1)/(2(x+1)))y+((x^2 +x−20)/(4(x+1)))=0)),((y^2 +((x^2 +6x+6)/(2x(x+1)))y+((3x−20)/(2x(x+1)))=0)) :} Subtract and solve for y y=−(((x−2)(x^2 +3x−20))/(2(x^3 −5x−6))) Insert and transform x^6 −35x^5 +34x^4 +500x^3 −784x^2 −680x+560=0 This has got 6 real solutions...

$$\mathrm{No}\:\mathrm{exact}\:\mathrm{solutions}\:\mathrm{possible}.\:\mathrm{Transform}\:\mathrm{to} \\ $$$$\begin{cases}{{y}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)}{y}+\frac{{x}^{\mathrm{2}} +{x}−\mathrm{20}}{\mathrm{4}\left({x}+\mathrm{1}\right)}=\mathrm{0}}\\{{y}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{6}}{\mathrm{2}{x}\left({x}+\mathrm{1}\right)}{y}+\frac{\mathrm{3}{x}−\mathrm{20}}{\mathrm{2}{x}\left({x}+\mathrm{1}\right)}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{Subtract}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}\:{y} \\ $$$${y}=−\frac{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{20}\right)}{\mathrm{2}\left({x}^{\mathrm{3}} −\mathrm{5}{x}−\mathrm{6}\right)} \\ $$$$\mathrm{Insert}\:\mathrm{and}\:\mathrm{transform} \\ $$$${x}^{\mathrm{6}} −\mathrm{35}{x}^{\mathrm{5}} +\mathrm{34}{x}^{\mathrm{4}} +\mathrm{500}{x}^{\mathrm{3}} −\mathrm{784}{x}^{\mathrm{2}} −\mathrm{680}{x}+\mathrm{560}=\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{has}\:\mathrm{got}\:\mathrm{6}\:\mathrm{real}\:\mathrm{solutions}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com