
Question Number 200299 by Calculusboy last updated on 16/Nov/23
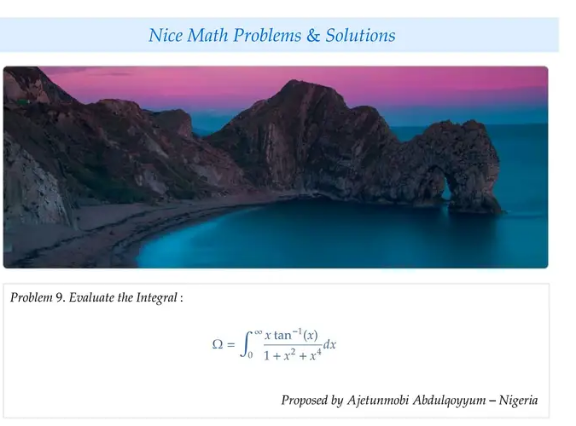
Answered by witcher3 last updated on 17/Nov/23
![x→(1/x) Ω=∫_∞ ^0 −(((tan^(−1) ((1/x)))/x)/(1+x^2 +x^4 )).(x^4 /x^2 )dx =∫_0 ^∞ ((x((π/2)−tan^(−1) (x)))/(x^4 +x^2 +1))dx =−Ω+(π/4)∫_0 ^∞ (dx^2 /((1+x^2 +x^4 )))=−Ω+(π/4)∫_0 ^∞ (dx/((x+(1/2))^2 +(3/4))) ⇔2Ω=(π/4).(2/( (√3)))tan^(−1) (((2x)/( (√3)))+(1/( (√3))))]_0 ^∞ =(π/(2(√3)))((π/2)−(π/6)) =(π^2 /(6(√3)))⇒Ω=(π^2 /(12(√3)))](Q200365.png)
$$\mathrm{x}\rightarrow\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\Omega=\int_{\infty} ^{\mathrm{0}} −\frac{\frac{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{x}}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{4}} }.\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$=−\Omega+\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{4}} \right)}=−\Omega+\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\left.\Leftrightarrow\mathrm{2}\Omega=\frac{\pi}{\mathrm{4}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}\sqrt{\mathrm{3}}}\Rightarrow\Omega=\frac{\pi^{\mathrm{2}} }{\mathrm{12}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Commented by Calculusboy last updated on 18/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
Commented by witcher3 last updated on 19/Nov/23

$$\mathrm{withe}\:\mathrm{Pleasur} \\ $$
