Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 200262 by sonukgindia last updated on 16/Nov/23

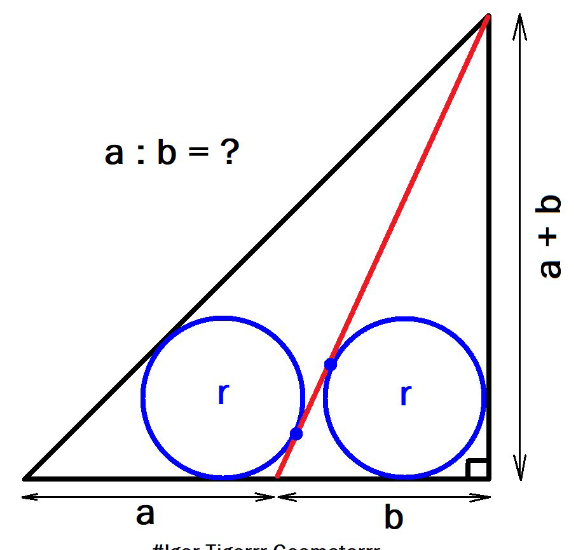
Answered by Frix last updated on 17/Nov/23

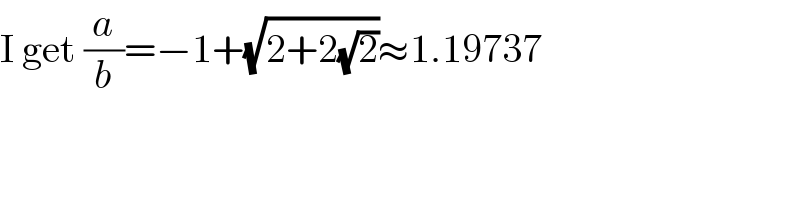
I get (a/b)=−1+(√(2+2(√2)))≈1.19737

$$\mathrm{I}\:\mathrm{get}\:\frac{{a}}{{b}}=−\mathrm{1}+\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}\approx\mathrm{1}.\mathrm{19737} \\ $$

Answered by mr W last updated on 17/Nov/23

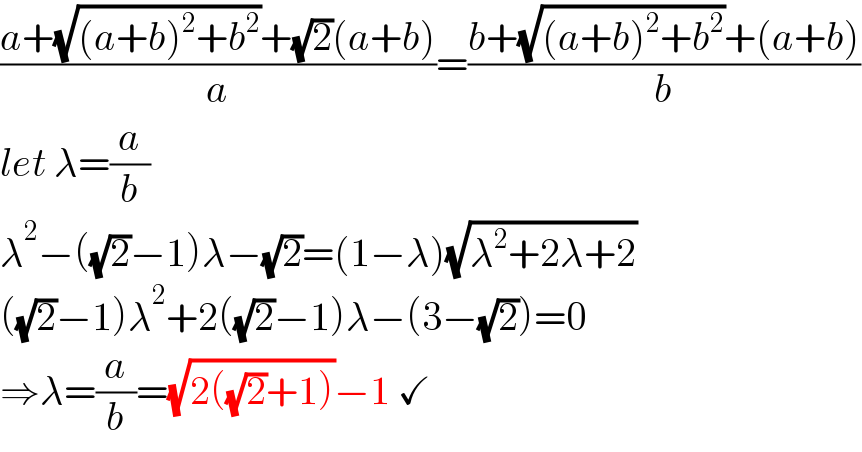
((a+(√((a+b)^2 +b^2 ))+(√2)(a+b))/a)=((b+(√((a+b)^2 +b^2 ))+(a+b))/b) let λ=(a/b) λ^2 −((√2)−1)λ−(√2)=(1−λ)(√(λ^2 +2λ+2)) ((√2)−1)λ^2 +2((√2)−1)λ−(3−(√2))=0 ⇒λ=(a/b)=(√(2((√2)+1)))−1 ✓

$$\frac{{a}+\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }+\sqrt{\mathrm{2}}\left({a}+{b}\right)}{{a}}=\frac{{b}+\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }+\left({a}+{b}\right)}{{b}} \\ $$$${let}\:\lambda=\frac{{a}}{{b}} \\ $$$$\lambda^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\lambda−\sqrt{\mathrm{2}}=\left(\mathrm{1}−\lambda\right)\sqrt{\lambda^{\mathrm{2}} +\mathrm{2}\lambda+\mathrm{2}} \\ $$$$\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\lambda^{\mathrm{2}} +\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\lambda−\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{a}}{{b}}=\sqrt{\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}−\mathrm{1}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com