Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 200242 by cherokeesay last updated on 16/Nov/23

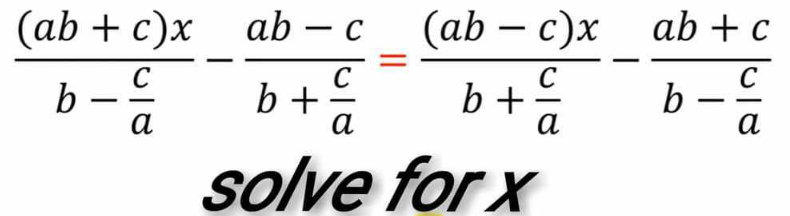
Answered by cortano12 last updated on 17/Nov/23

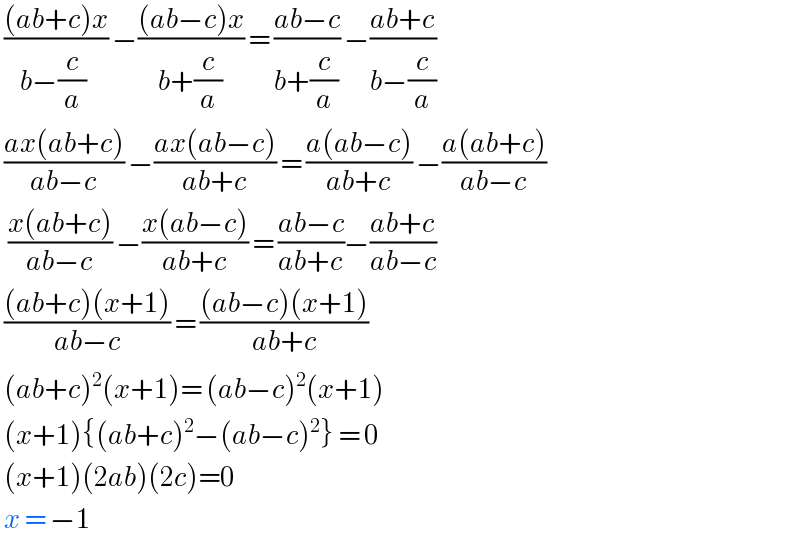
(((ab+c)x)/(b−(c/a) )) −(((ab−c)x)/(b+(c/a))) = ((ab−c)/(b+(c/a))) −((ab+c)/(b−(c/a))) ((ax(ab+c))/(ab−c)) −((ax(ab−c))/(ab+c)) = ((a(ab−c))/(ab+c)) −((a(ab+c))/(ab−c)) ((x(ab+c))/(ab−c)) −((x(ab−c))/(ab+c)) = ((ab−c)/(ab+c))−((ab+c)/(ab−c)) (((ab+c)(x+1))/(ab−c)) = (((ab−c)(x+1))/(ab+c)) (ab+c)^2 (x+1)= (ab−c)^2 (x+1) (x+1){(ab+c)^2 −(ab−c)^2 } = 0 (x+1)(2ab)(2c)=0 x = −1

$$\:\frac{\left({ab}+{c}\right){x}}{{b}−\frac{{c}}{{a}}\:}\:−\frac{\left({ab}−{c}\right){x}}{{b}+\frac{{c}}{{a}}}\:=\:\frac{{ab}−{c}}{{b}+\frac{{c}}{{a}}}\:−\frac{{ab}+{c}}{{b}−\frac{{c}}{{a}}} \\ $$$$\:\frac{{ax}\left({ab}+{c}\right)}{{ab}−{c}}\:−\frac{{ax}\left({ab}−{c}\right)}{{ab}+{c}}\:=\:\frac{{a}\left({ab}−{c}\right)}{{ab}+{c}}\:−\frac{{a}\left({ab}+{c}\right)}{{ab}−{c}} \\ $$$$\:\:\frac{{x}\left({ab}+{c}\right)}{{ab}−{c}}\:−\frac{{x}\left({ab}−{c}\right)}{{ab}+{c}}\:=\:\frac{{ab}−{c}}{{ab}+{c}}−\frac{{ab}+{c}}{{ab}−{c}} \\ $$$$\:\frac{\left({ab}+{c}\right)\left({x}+\mathrm{1}\right)}{{ab}−{c}}\:=\:\frac{\left({ab}−{c}\right)\left({x}+\mathrm{1}\right)}{{ab}+{c}} \\ $$$$\:\left({ab}+{c}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)=\:\left({ab}−{c}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right) \\ $$$$\:\left({x}+\mathrm{1}\right)\left\{\left({ab}+{c}\right)^{\mathrm{2}} −\left({ab}−{c}\right)^{\mathrm{2}} \right\}\:=\:\mathrm{0} \\ $$$$\:\left({x}+\mathrm{1}\right)\left(\mathrm{2}{ab}\right)\left(\mathrm{2}{c}\right)=\mathrm{0} \\ $$$$\:{x}\:=\:−\mathrm{1} \\ $$

Commented by cherokeesay last updated on 16/Nov/23

thanks !

$${thanks}\:! \\ $$

Answered by som(math1967) last updated on 16/Nov/23

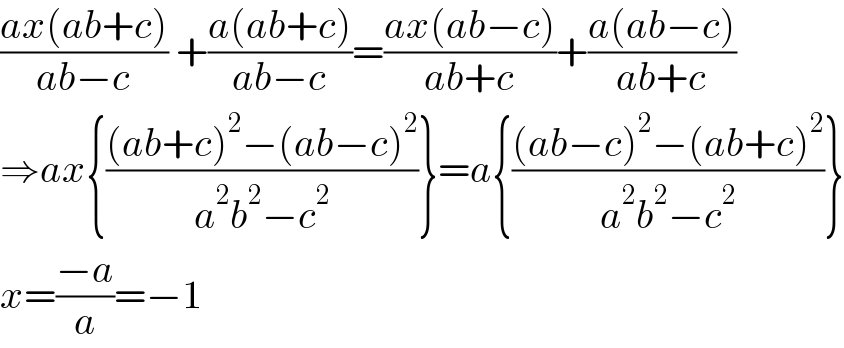
((ax(ab+c))/(ab−c)) +((a(ab+c))/(ab−c))=((ax(ab−c))/(ab+c))+((a(ab−c))/(ab+c)) ⇒ax{(((ab+c)^2 −(ab−c)^2 )/(a^2 b^2 −c^2 ))}=a{(((ab−c)^2 −(ab+c)^2 )/(a^2 b^2 −c^2 ))} x=((−a)/a)=−1

$$\frac{{ax}\left({ab}+{c}\right)}{{ab}−{c}}\:+\frac{{a}\left({ab}+{c}\right)}{{ab}−{c}}=\frac{{ax}\left({ab}−{c}\right)}{{ab}+{c}}+\frac{{a}\left({ab}−{c}\right)}{{ab}+{c}} \\ $$$$\Rightarrow{ax}\left\{\frac{\left({ab}+{c}\right)^{\mathrm{2}} −\left({ab}−{c}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} −{c}^{\mathrm{2}} }\right\}={a}\left\{\frac{\left({ab}−{c}\right)^{\mathrm{2}} −\left({ab}+{c}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} −{c}^{\mathrm{2}} }\right\} \\ $$$${x}=\frac{−{a}}{{a}}=−\mathrm{1}\: \\ $$

Commented by cherokeesay last updated on 16/Nov/23

thank you !

$${thank}\:{you}\:! \\ $$

Answered by Rasheed.Sindhi last updated on 16/Nov/23

(((ab+c)x)/(b−(c/a)))−((ab−c)/(b+(c/a)))=(((ab−c)x)/(b+(c/a)))−((ab+c)/(b−(c/a))) (((ab+c)/(b−(c/a)))−((ab−c)/(b+(c/a))))x=((ab−c)/(b+(c/a)))−((ab+c)/(b−(c/a))) a(((b+(c/a))/(b−(c/a)))−((b−(c/a))/(b+(c/a))))x=−a(((b+(c/a))/(b−(c/a)))−((b−(c/a))/(b+(c/a)))) [a≠0] x=−1

$$\frac{\left({ab}+{c}\right){x}}{{b}−\frac{{c}}{{a}}}−\frac{{ab}−{c}}{{b}+\frac{{c}}{{a}}}=\frac{\left({ab}−{c}\right){x}}{{b}+\frac{{c}}{{a}}}−\frac{{ab}+{c}}{{b}−\frac{{c}}{{a}}} \\ $$$$\left(\frac{{ab}+{c}}{{b}−\frac{{c}}{{a}}}−\frac{{ab}−{c}}{{b}+\frac{{c}}{{a}}}\right){x}=\frac{{ab}−{c}}{{b}+\frac{{c}}{{a}}}−\frac{{ab}+{c}}{{b}−\frac{{c}}{{a}}} \\ $$$$\cancel{{a}}\left(\frac{{b}+\frac{{c}}{{a}}}{{b}−\frac{{c}}{{a}}}−\frac{{b}−\frac{{c}}{{a}}}{{b}+\frac{{c}}{{a}}}\right){x}=−\cancel{{a}}\left(\frac{{b}+\frac{{c}}{{a}}}{{b}−\frac{{c}}{{a}}}−\frac{{b}−\frac{{c}}{{a}}}{{b}+\frac{{c}}{{a}}}\right)\:\:\:\left[{a}\neq\mathrm{0}\right] \\ $$$${x}=−\mathrm{1} \\ $$

Commented by cherokeesay last updated on 16/Nov/23

thank you !

$${thank}\:{you}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com