Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 200025 by cortano12 last updated on 12/Nov/23

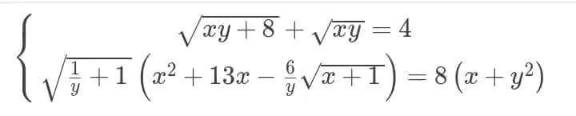
Answered by Frix last updated on 12/Nov/23

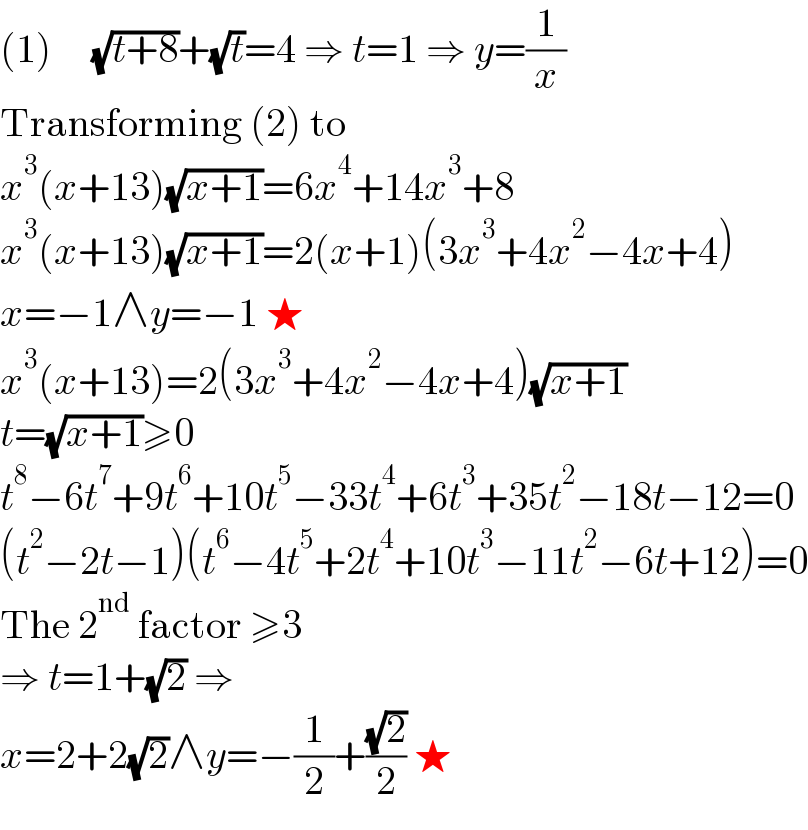
(1) (√(t+8))+(√t)=4 ⇒ t=1 ⇒ y=(1/x) Transforming (2) to x^3 (x+13)(√(x+1))=6x^4 +14x^3 +8 x^3 (x+13)(√(x+1))=2(x+1)(3x^3 +4x^2 −4x+4) x=−1∧y=−1 ★ x^3 (x+13)=2(3x^3 +4x^2 −4x+4)(√(x+1)) t=(√(x+1))≥0 t^8 −6t^7 +9t^6 +10t^5 −33t^4 +6t^3 +35t^2 −18t−12=0 (t^2 −2t−1)(t^6 −4t^5 +2t^4 +10t^3 −11t^2 −6t+12)=0 The 2^(nd) factor ≥3 ⇒ t=1+(√2) ⇒ x=2+2(√2)∧y=−(1/2)+((√2)/2) ★

$$\left(\mathrm{1}\right)\:\:\:\:\:\sqrt{{t}+\mathrm{8}}+\sqrt{{t}}=\mathrm{4}\:\Rightarrow\:{t}=\mathrm{1}\:\Rightarrow\:{y}=\frac{\mathrm{1}}{{x}} \\ $$$$\mathrm{Transforming}\:\left(\mathrm{2}\right)\:\mathrm{to} \\ $$$${x}^{\mathrm{3}} \left({x}+\mathrm{13}\right)\sqrt{{x}+\mathrm{1}}=\mathrm{6}{x}^{\mathrm{4}} +\mathrm{14}{x}^{\mathrm{3}} +\mathrm{8} \\ $$$${x}^{\mathrm{3}} \left({x}+\mathrm{13}\right)\sqrt{{x}+\mathrm{1}}=\mathrm{2}\left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right) \\ $$$${x}=−\mathrm{1}\wedge{y}=−\mathrm{1}\:\bigstar \\ $$$${x}^{\mathrm{3}} \left({x}+\mathrm{13}\right)=\mathrm{2}\left(\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)\sqrt{{x}+\mathrm{1}} \\ $$$${t}=\sqrt{{x}+\mathrm{1}}\geqslant\mathrm{0} \\ $$$${t}^{\mathrm{8}} −\mathrm{6}{t}^{\mathrm{7}} +\mathrm{9}{t}^{\mathrm{6}} +\mathrm{10}{t}^{\mathrm{5}} −\mathrm{33}{t}^{\mathrm{4}} +\mathrm{6}{t}^{\mathrm{3}} +\mathrm{35}{t}^{\mathrm{2}} −\mathrm{18}{t}−\mathrm{12}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{6}} −\mathrm{4}{t}^{\mathrm{5}} +\mathrm{2}{t}^{\mathrm{4}} +\mathrm{10}{t}^{\mathrm{3}} −\mathrm{11}{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{12}\right)=\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{factor}\:\geqslant\mathrm{3} \\ $$$$\Rightarrow\:{t}=\mathrm{1}+\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$${x}=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\wedge{y}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\bigstar \\ $$

Answered by Rasheed.Sindhi last updated on 12/Nov/23

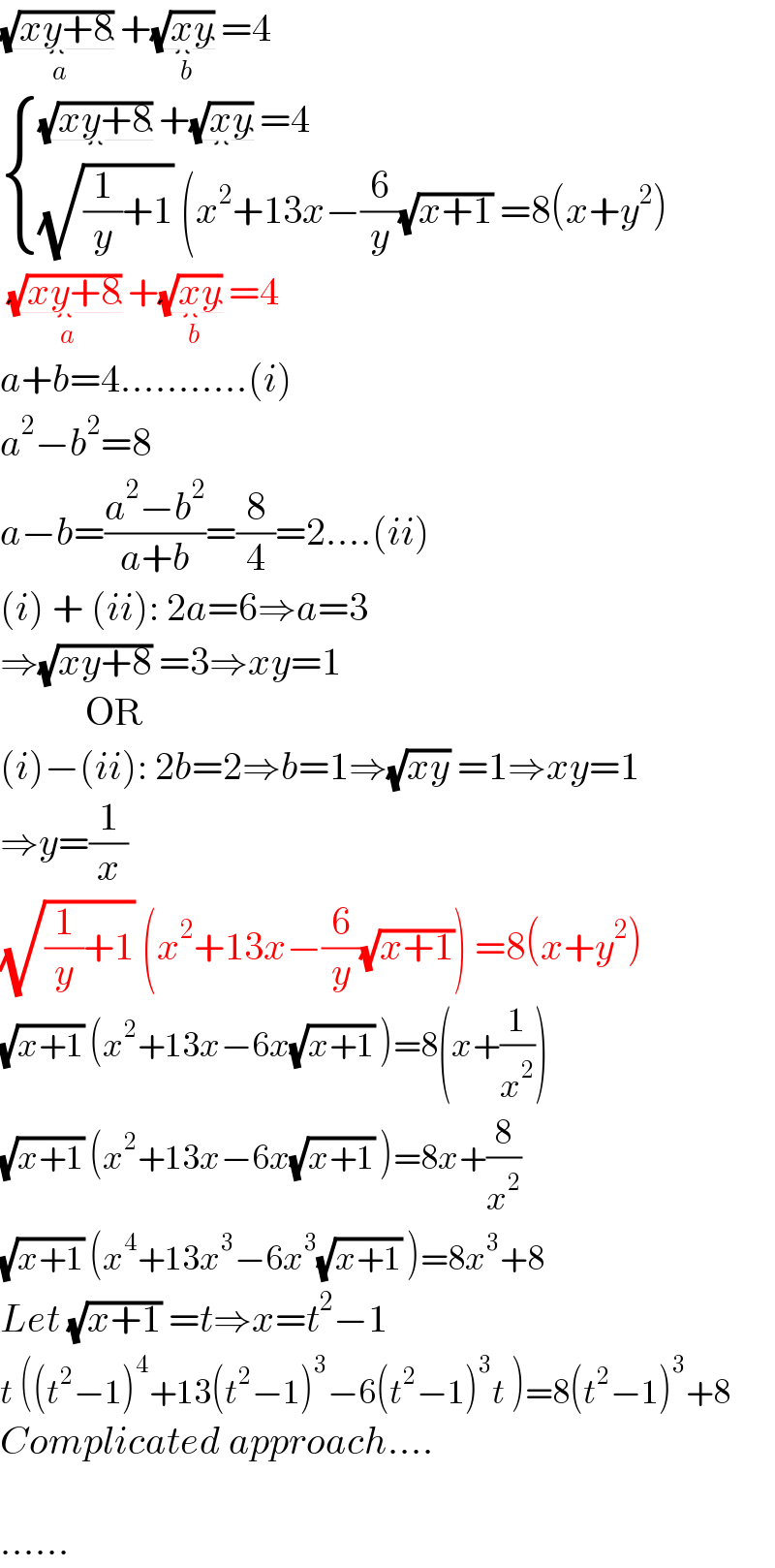
(√(xy+8)) _(a) +(√(xy)) _(b) =4 { (((√(xy+8)) +(√(xy)) =4)),(((√((1/y)+1)) (x^2 +13x−(6/y)(√(x+1)) =8(x+y^2 ))) :} (√(xy+8)) _(a) +(√(xy)) _(b) =4 a+b=4...........(i) a^2 −b^2 =8 a−b=((a^2 −b^2 )/(a+b))=(8/4)=2....(ii) (i) + (ii): 2a=6⇒a=3 ⇒(√(xy+8)) =3⇒xy=1 OR (i)−(ii): 2b=2⇒b=1⇒(√(xy)) =1⇒xy=1 ⇒y=(1/x) (√((1/y)+1)) (x^2 +13x−(6/y)(√(x+1))) =8(x+y^2 ) (√(x+1)) (x^2 +13x−6x(√(x+1)) )=8(x+(1/x^2 )) (√(x+1)) (x^2 +13x−6x(√(x+1)) )=8x+(8/x^2 ) (√(x+1)) (x^4 +13x^3 −6x^3 (√(x+1)) )=8x^3 +8 Let (√(x+1)) =t⇒x=t^2 −1 t ((t^2 −1)^4 +13(t^2 −1)^3 −6(t^2 −1)^3 t )=8(t^2 −1)^3 +8 Complicated approach.... ......

$$\underset{{a}} {\underbrace{\sqrt{{xy}+\mathrm{8}}\:}}+\underset{{b}} {\underbrace{\sqrt{{xy}}\:}}=\mathrm{4} \\ $$$$\begin{cases}{\underbrace{\sqrt{{xy}+\mathrm{8}}\:}+\underbrace{\sqrt{{xy}}\:}=\mathrm{4}}\\{\sqrt{\frac{\mathrm{1}}{{y}}+\mathrm{1}}\:\left({x}^{\mathrm{2}} +\mathrm{13}{x}−\frac{\mathrm{6}}{{y}}\sqrt{{x}+\mathrm{1}}\:=\mathrm{8}\left({x}+{y}^{\mathrm{2}} \right)\right.}\end{cases} \\ $$$$\:\underset{{a}} {\underbrace{\sqrt{{xy}+\mathrm{8}}\:}}+\underset{{b}} {\underbrace{\sqrt{{xy}}\:}}=\mathrm{4} \\ $$$${a}+{b}=\mathrm{4}...........\left({i}\right) \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{8} \\ $$$${a}−{b}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}+{b}}=\frac{\mathrm{8}}{\mathrm{4}}=\mathrm{2}....\left({ii}\right) \\ $$$$\left({i}\right)\:+\:\left({ii}\right):\:\mathrm{2}{a}=\mathrm{6}\Rightarrow{a}=\mathrm{3} \\ $$$$\Rightarrow\sqrt{{xy}+\mathrm{8}}\:=\mathrm{3}\Rightarrow{xy}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{OR} \\ $$$$\left({i}\right)−\left({ii}\right):\:\mathrm{2}{b}=\mathrm{2}\Rightarrow{b}=\mathrm{1}\Rightarrow\sqrt{{xy}}\:=\mathrm{1}\Rightarrow{xy}=\mathrm{1} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{{x}} \\ $$$$\sqrt{\frac{\mathrm{1}}{{y}}+\mathrm{1}}\:\left({x}^{\mathrm{2}} +\mathrm{13}{x}−\frac{\mathrm{6}}{{y}}\sqrt{{x}+\mathrm{1}}\right)\:=\mathrm{8}\left({x}+{y}^{\mathrm{2}} \right) \\ $$$$\sqrt{{x}+\mathrm{1}}\:\left({x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{6}{x}\sqrt{{x}+\mathrm{1}}\:\right)=\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\sqrt{{x}+\mathrm{1}}\:\left({x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{6}{x}\sqrt{{x}+\mathrm{1}}\:\right)=\mathrm{8}{x}+\frac{\mathrm{8}}{{x}^{\mathrm{2}} } \\ $$$$\sqrt{{x}+\mathrm{1}}\:\left({x}^{\mathrm{4}} +\mathrm{13}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\:\right)=\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8} \\ $$$${Let}\:\sqrt{{x}+\mathrm{1}}\:={t}\Rightarrow{x}={t}^{\mathrm{2}} −\mathrm{1} \\ $$$${t}\:\left(\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{4}} +\mathrm{13}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} −\mathrm{6}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} {t}\:\right)=\mathrm{8}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} +\mathrm{8} \\ $$$${Complicated}\:{approach}.... \\ $$$$ \\ $$$$...... \\ $$

Answered by MathematicalUser2357 last updated on 15/Nov/23

Yay, 200K!

$$\mathrm{Yay},\:\mathrm{200K}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com