Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199923 by Rupesh123 last updated on 11/Nov/23

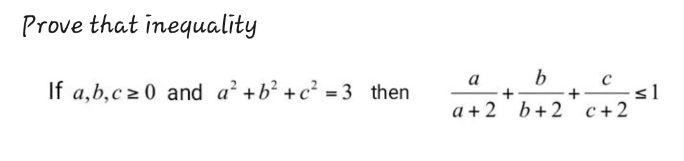
Answered by deleteduser1 last updated on 11/Nov/23

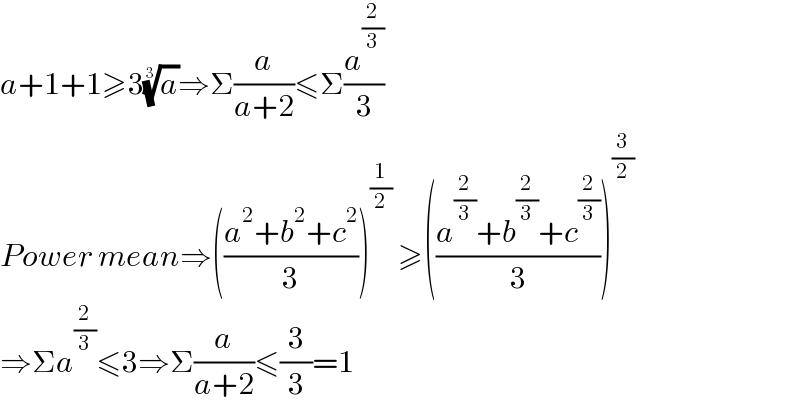
a+1+1≥3(a)^(1/3) ⇒Σ(a/(a+2))≤Σ(a^(2/3) /3) Power mean⇒(((a^2 +b^2 +c^2 )/3))^(1/2) ≥(((a^(2/3) +b^(2/3) +c^(2/3) )/3))^(3/2) ⇒Σa^(2/3) ≤3⇒Σ(a/(a+2))≤(3/3)=1

$${a}+\mathrm{1}+\mathrm{1}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{{a}}\Rightarrow\Sigma\frac{{a}}{{a}+\mathrm{2}}\leqslant\Sigma\frac{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{3}} \\ $$$${Power}\:{mean}\Rightarrow\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\geqslant\left(\frac{{a}^{\frac{\mathrm{2}}{\mathrm{3}}} +{b}^{\frac{\mathrm{2}}{\mathrm{3}}} +{c}^{\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{3}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow\Sigma{a}^{\frac{\mathrm{2}}{\mathrm{3}}} \leqslant\mathrm{3}\Rightarrow\Sigma\frac{{a}}{{a}+\mathrm{2}}\leqslant\frac{\mathrm{3}}{\mathrm{3}}=\mathrm{1} \\ $$

Commented by Rupesh123 last updated on 11/Nov/23

Very elegant, sir!

Answered by witcher3 last updated on 12/Nov/23

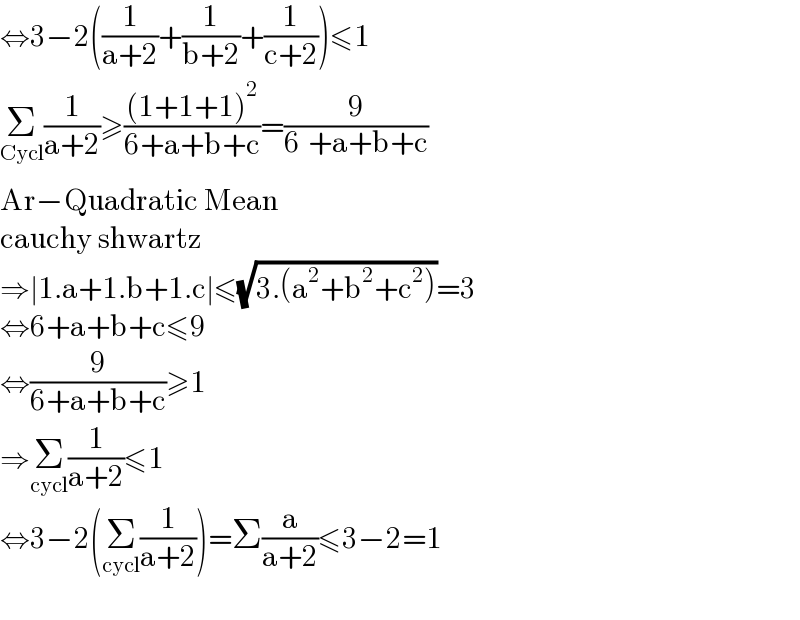
⇔3−2((1/(a+2))+(1/(b+2))+(1/(c+2)))≤1 Σ_(Cycl) (1/(a+2))≥(((1+1+1)^2 )/(6+a+b+c))=(9/(6_ +a+b+c)) Ar−Quadratic Mean cauchy shwartz ⇒∣1.a+1.b+1.c∣≤(√(3.(a^2 +b^2 +c^2 )))=3 ⇔6+a+b+c≤9 ⇔(9/(6+a+b+c))≥1 ⇒Σ_(cycl) (1/(a+2))≤1 ⇔3−2(Σ_(cycl) (1/(a+2)))=Σ(a/(a+2))≤3−2=1

$$\Leftrightarrow\mathrm{3}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{a}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{b}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{c}+\mathrm{2}}\right)\leqslant\mathrm{1} \\ $$$$\underset{\mathrm{Cycl}} {\sum}\frac{\mathrm{1}}{\mathrm{a}+\mathrm{2}}\geqslant\frac{\left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{6}+\mathrm{a}+\mathrm{b}+\mathrm{c}}=\frac{\mathrm{9}}{\mathrm{6}_{} +\mathrm{a}+\mathrm{b}+\mathrm{c}} \\ $$$$\mathrm{Ar}−\mathrm{Quadratic}\:\mathrm{Mean} \\ $$$$\mathrm{cauchy}\:\mathrm{shwartz}\: \\ $$$$\Rightarrow\mid\mathrm{1}.\mathrm{a}+\mathrm{1}.\mathrm{b}+\mathrm{1}.\mathrm{c}\mid\leqslant\sqrt{\mathrm{3}.\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}=\mathrm{3} \\ $$$$\Leftrightarrow\mathrm{6}+\mathrm{a}+\mathrm{b}+\mathrm{c}\leqslant\mathrm{9} \\ $$$$\Leftrightarrow\frac{\mathrm{9}}{\mathrm{6}+\mathrm{a}+\mathrm{b}+\mathrm{c}}\geqslant\mathrm{1} \\ $$$$\Rightarrow\underset{\mathrm{cycl}} {\sum}\frac{\mathrm{1}}{\mathrm{a}+\mathrm{2}}\leqslant\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{3}−\mathrm{2}\left(\underset{\mathrm{cycl}} {\sum}\frac{\mathrm{1}}{\mathrm{a}+\mathrm{2}}\right)=\Sigma\frac{\mathrm{a}}{\mathrm{a}+\mathrm{2}}\leqslant\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com