
Question Number 199854 by sonukgindia last updated on 10/Nov/23
Answered by aleks041103 last updated on 10/Nov/23
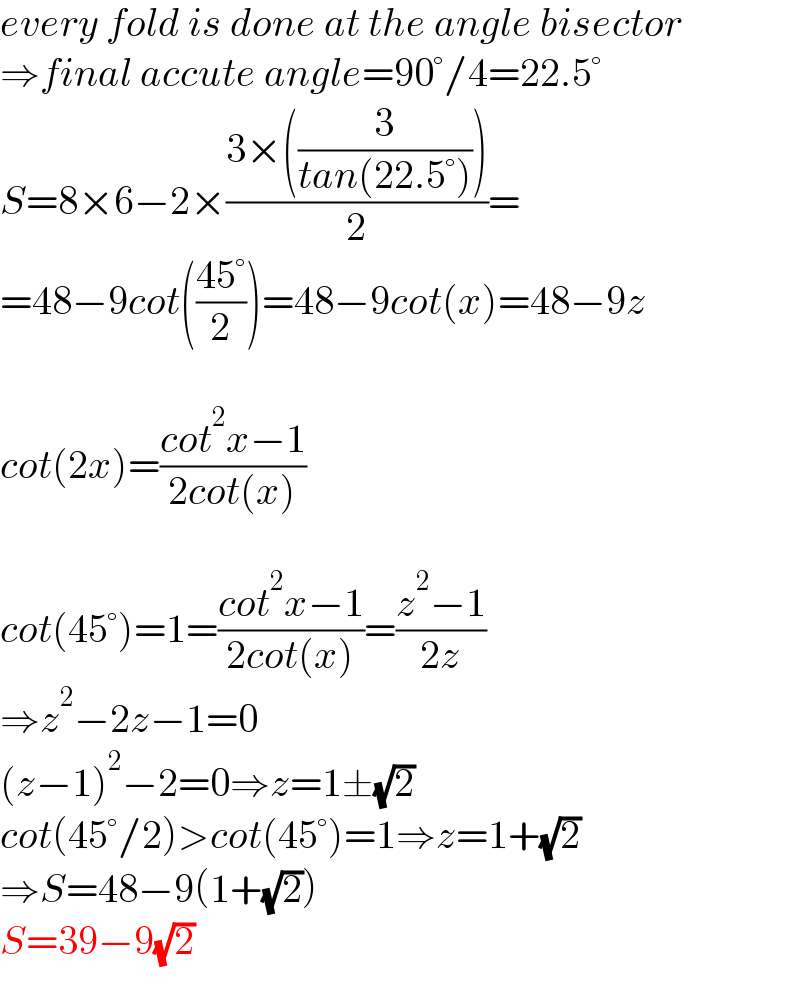
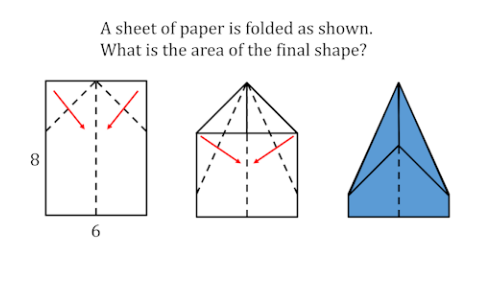
$${every}\:{fold}\:{is}\:{done}\:{at}\:{the}\:{angle}\:{bisector} \\ $$$$\Rightarrow{final}\:{accute}\:{angle}=\mathrm{90}°/\mathrm{4}=\mathrm{22}.\mathrm{5}° \\ $$$${S}=\mathrm{8}×\mathrm{6}−\mathrm{2}×\frac{\mathrm{3}×\left(\frac{\mathrm{3}}{{tan}\left(\mathrm{22}.\mathrm{5}°\right)}\right)}{\mathrm{2}}= \\ $$$$=\mathrm{48}−\mathrm{9}{cot}\left(\frac{\mathrm{45}°}{\mathrm{2}}\right)=\mathrm{48}−\mathrm{9}{cot}\left({x}\right)=\mathrm{48}−\mathrm{9}{z} \\ $$$$ \\ $$$${cot}\left(\mathrm{2}{x}\right)=\frac{{cot}^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{2}{cot}\left({x}\right)} \\ $$$$ \\ $$$${cot}\left(\mathrm{45}°\right)=\mathrm{1}=\frac{{cot}^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{2}{cot}\left({x}\right)}=\frac{{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{z}} \\ $$$$\Rightarrow{z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{1}=\mathrm{0} \\ $$$$\left({z}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{0}\Rightarrow{z}=\mathrm{1}\pm\sqrt{\mathrm{2}} \\ $$$${cot}\left(\mathrm{45}°/\mathrm{2}\right)>{cot}\left(\mathrm{45}°\right)=\mathrm{1}\Rightarrow{z}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{S}=\mathrm{48}−\mathrm{9}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${S}=\mathrm{39}−\mathrm{9}\sqrt{\mathrm{2}} \\ $$
