Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199774 by Mingma last updated on 09/Nov/23

Answered by ajfour last updated on 09/Nov/23

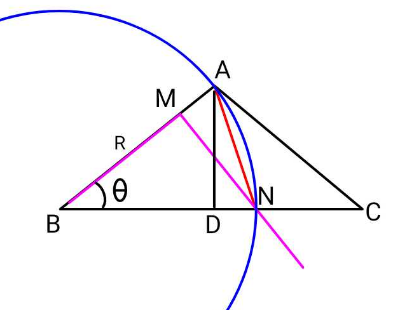
Commented by ajfour last updated on 09/Nov/23

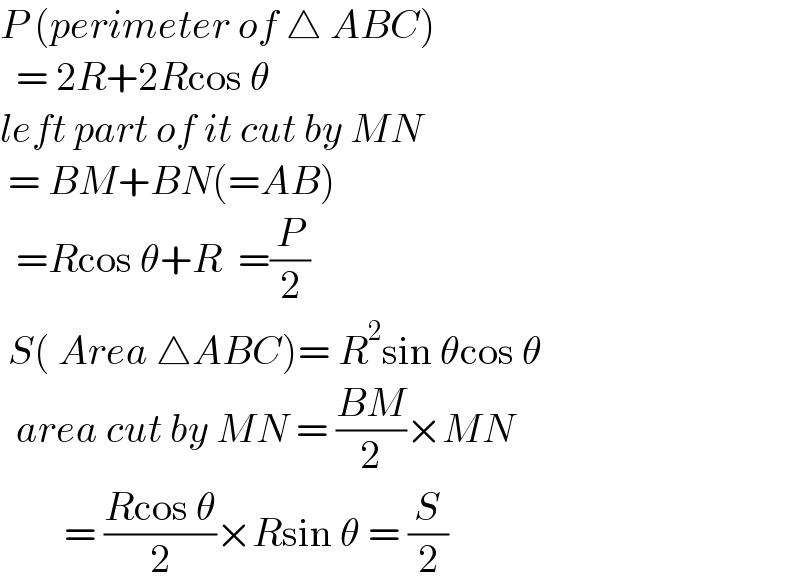
P (perimeter of △ ABC) = 2R+2Rcos θ left part of it cut by MN = BM+BN(=AB) =Rcos θ+R =(P/2) S( Area △ABC)= R^2 sin θcos θ area cut by MN = ((BM)/2)×MN = ((Rcos θ)/2)×Rsin θ = (S/2)

$${P}\:\left({perimeter}\:{of}\:\bigtriangleup\:{ABC}\right) \\ $$$$\:\:=\:\mathrm{2}{R}+\mathrm{2}{R}\mathrm{cos}\:\theta \\ $$$${left}\:{part}\:{of}\:{it}\:{cut}\:{by}\:{MN} \\ $$$$\:=\:{BM}+{BN}\left(={AB}\right) \\ $$$$\:\:={R}\mathrm{cos}\:\theta+{R}\:\:=\frac{{P}}{\mathrm{2}} \\ $$$$\:{S}\left(\:{Area}\:\bigtriangleup{ABC}\right)=\:{R}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\:\:{area}\:{cut}\:{by}\:{MN}\:=\:\frac{{BM}}{\mathrm{2}}×{MN} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{{R}\mathrm{cos}\:\theta}{\mathrm{2}}×{R}\mathrm{sin}\:\theta\:=\:\frac{{S}}{\mathrm{2}} \\ $$

Commented by Mingma last updated on 09/Nov/23

Very elegant solution!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com