
Question Number 199671 by Mingma last updated on 07/Nov/23

Answered by mr W last updated on 07/Nov/23
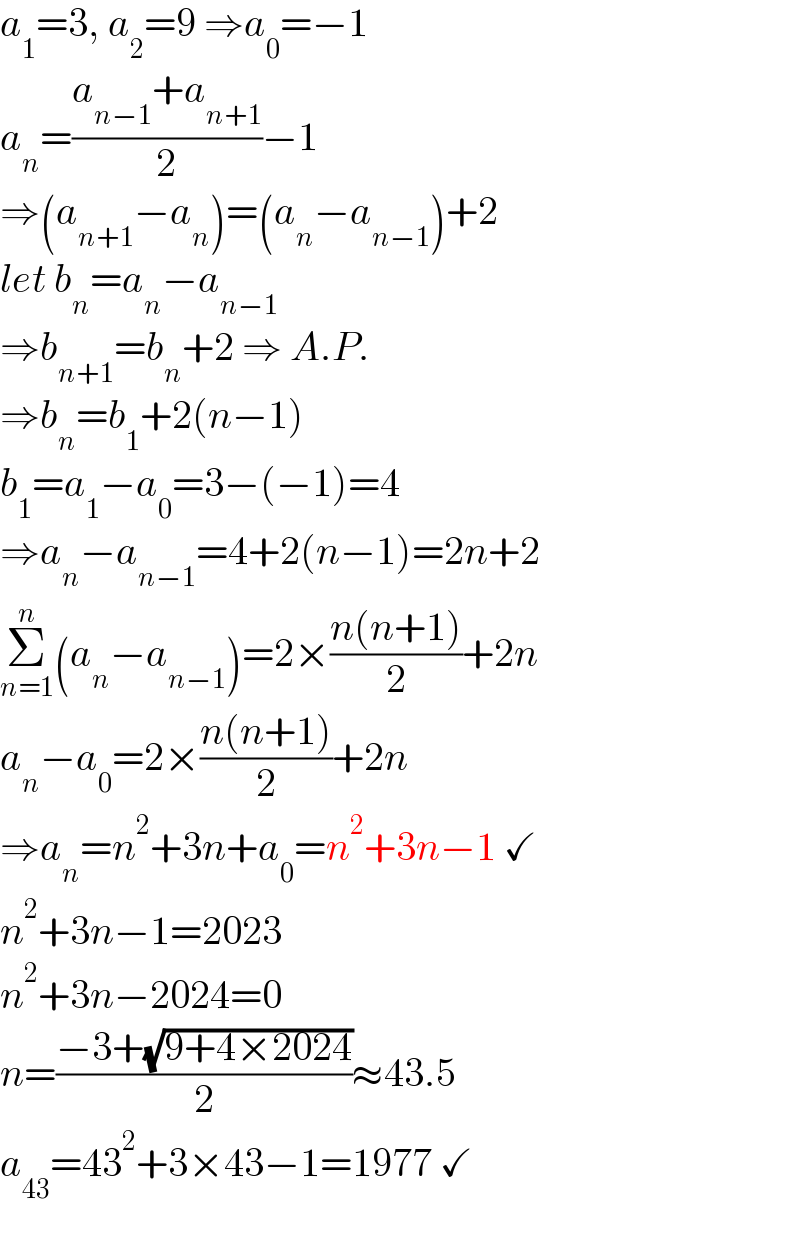
$${a}_{\mathrm{1}} =\mathrm{3},\:{a}_{\mathrm{2}} =\mathrm{9}\:\Rightarrow{a}_{\mathrm{0}} =−\mathrm{1} \\ $$$${a}_{{n}} =\frac{{a}_{{n}−\mathrm{1}} +{a}_{{n}+\mathrm{1}} }{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow\left({a}_{{n}+\mathrm{1}} −{a}_{{n}} \right)=\left({a}_{{n}} −{a}_{{n}−\mathrm{1}} \right)+\mathrm{2} \\ $$$${let}\:{b}_{{n}} ={a}_{{n}} −{a}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} ={b}_{{n}} +\mathrm{2}\:\Rightarrow\:{A}.{P}. \\ $$$$\Rightarrow{b}_{{n}} ={b}_{\mathrm{1}} +\mathrm{2}\left({n}−\mathrm{1}\right) \\ $$$${b}_{\mathrm{1}} ={a}_{\mathrm{1}} −{a}_{\mathrm{0}} =\mathrm{3}−\left(−\mathrm{1}\right)=\mathrm{4} \\ $$$$\Rightarrow{a}_{{n}} −{a}_{{n}−\mathrm{1}} =\mathrm{4}+\mathrm{2}\left({n}−\mathrm{1}\right)=\mathrm{2}{n}+\mathrm{2} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left({a}_{{n}} −{a}_{{n}−\mathrm{1}} \right)=\mathrm{2}×\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\mathrm{2}{n} \\ $$$${a}_{{n}} −{a}_{\mathrm{0}} =\mathrm{2}×\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\mathrm{2}{n} \\ $$$$\Rightarrow{a}_{{n}} ={n}^{\mathrm{2}} +\mathrm{3}{n}+{a}_{\mathrm{0}} ={n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}\:\checkmark \\ $$$${n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}=\mathrm{2023} \\ $$$${n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{2024}=\mathrm{0} \\ $$$${n}=\frac{−\mathrm{3}+\sqrt{\mathrm{9}+\mathrm{4}×\mathrm{2024}}}{\mathrm{2}}\approx\mathrm{43}.\mathrm{5} \\ $$$${a}_{\mathrm{43}} =\mathrm{43}^{\mathrm{2}} +\mathrm{3}×\mathrm{43}−\mathrm{1}=\mathrm{1977}\:\checkmark \\ $$
Commented by Mingma last updated on 07/Nov/23
Perfect ��
