
Question Number 199568 by ajfour last updated on 05/Nov/23
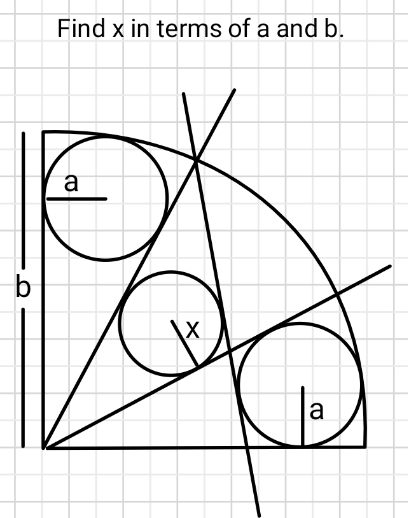
Commented by ajfour last updated on 05/Nov/23
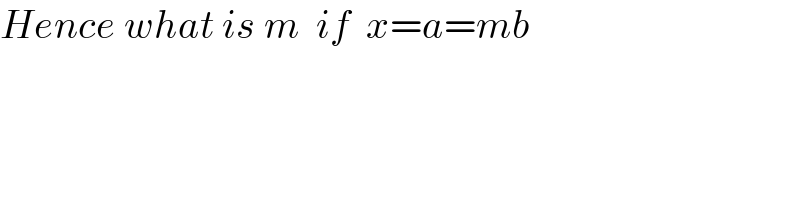
$${Hence}\:{what}\:{is}\:{m}\:\:{if}\:\:{x}={a}={mb} \\ $$
Answered by ajfour last updated on 05/Nov/23
![sin α=(a/(b−a)) x^2 +y^2 =b^2 A(bsin 2α, bcos 2α) centre of X circle (p,p) & radius r Q[(b−a)cos α, a] let y−bcos 2α=m(x−bsin 2α) (({a−bcos 2α−m[(b−a)cos α−bsin 2α]})/( (√(1+m^2 ))))=a even p−bcos 2α−m[p−bsin 2α]=r(√(1+m^2 )) so we found m<0 then p>0 r=p(√2)sin ((π/4)−2α)](Q199582.png)
$$\mathrm{sin}\:\alpha=\frac{{a}}{{b}−{a}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${A}\left({b}\mathrm{sin}\:\mathrm{2}\alpha,\:{b}\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$${centre}\:{of}\:{X}\:{circle}\:\left({p},{p}\right)\:\:\&\:{radius}\:{r} \\ $$$${Q}\left[\left({b}−{a}\right)\mathrm{cos}\:\alpha,\:{a}\right] \\ $$$${let}\:\:\:{y}−{b}\mathrm{cos}\:\mathrm{2}\alpha={m}\left({x}−{b}\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$$$\frac{\left\{{a}−{b}\mathrm{cos}\:\mathrm{2}\alpha−{m}\left[\left({b}−{a}\right)\mathrm{cos}\:\alpha−{b}\mathrm{sin}\:\mathrm{2}\alpha\right]\right\}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}={a} \\ $$$${even} \\ $$$${p}−{b}\mathrm{cos}\:\mathrm{2}\alpha−{m}\left[{p}−{b}\mathrm{sin}\:\mathrm{2}\alpha\right]={r}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${so}\:{we}\:{found}\:{m}<\mathrm{0}\:\:{then}\:{p}>\mathrm{0} \\ $$$${r}={p}\sqrt{\mathrm{2}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−\mathrm{2}\alpha\right) \\ $$$$ \\ $$
Commented by ajfour last updated on 05/Nov/23
https://youtu.be/QoHc39Vmp3E?si=WaxfcQ7XGn5uEq2b
Commented by ajfour last updated on 05/Nov/23
$${my}\:{lecture}\:{parabola}\:\mathrm{3} \\ $$
