Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199509 by hardmath last updated on 04/Nov/23

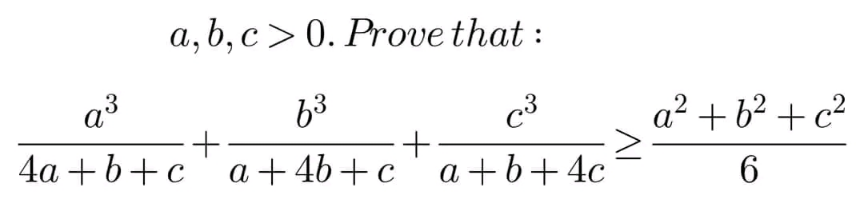
Commented by York12 last updated on 04/Nov/23

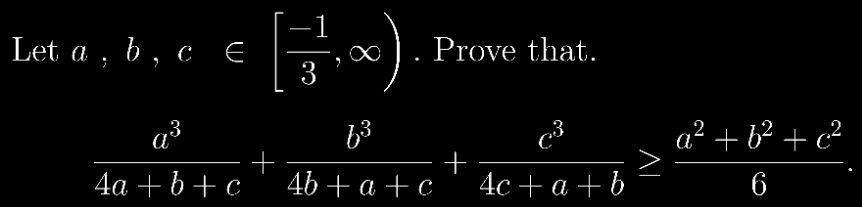
Commented by York12 last updated on 04/Nov/23

That is more general

$$\mathrm{That}\:\mathrm{is}\:\mathrm{more}\:\mathrm{general}\: \\ $$

Answered by deleteduser1 last updated on 04/Nov/23

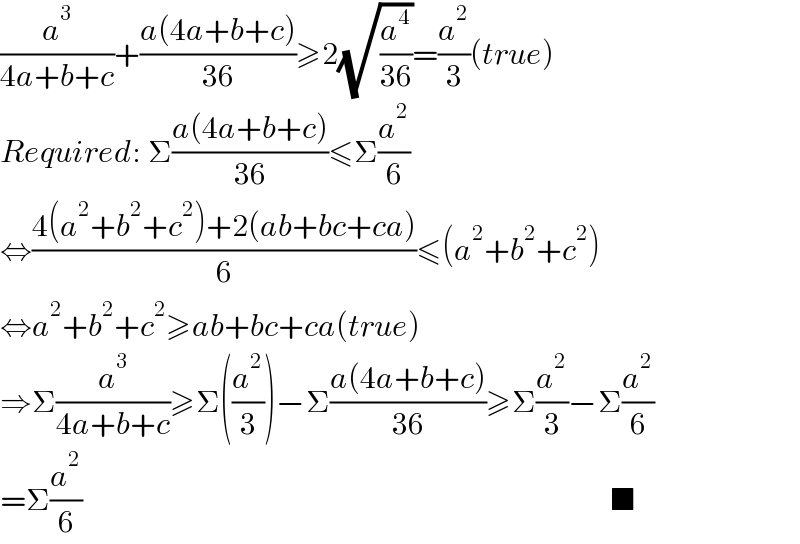
(a^3 /(4a+b+c))+((a(4a+b+c))/(36))≥2(√(a^4 /(36)))=(a^2 /3)(true) Required: Σ((a(4a+b+c))/(36))≤Σ(a^2 /6) ⇔((4(a^2 +b^2 +c^2 )+2(ab+bc+ca))/6)≤(a^2 +b^2 +c^2 ) ⇔a^2 +b^2 +c^2 ≥ab+bc+ca(true) ⇒Σ(a^3 /(4a+b+c))≥Σ((a^2 /3))−Σ((a(4a+b+c))/(36))≥Σ(a^2 /3)−Σ(a^2 /6) =Σ(a^2 /6) ■

$$\frac{{a}^{\mathrm{3}} }{\mathrm{4}{a}+{b}+{c}}+\frac{{a}\left(\mathrm{4}{a}+{b}+{c}\right)}{\mathrm{36}}\geqslant\mathrm{2}\sqrt{\frac{{a}^{\mathrm{4}} }{\mathrm{36}}}=\frac{{a}^{\mathrm{2}} }{\mathrm{3}}\left({true}\right) \\ $$$${Required}:\:\Sigma\frac{{a}\left(\mathrm{4}{a}+{b}+{c}\right)}{\mathrm{36}}\leqslant\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Leftrightarrow\frac{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\left({ab}+{bc}+{ca}\right)}{\mathrm{6}}\leqslant\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \geqslant{ab}+{bc}+{ca}\left({true}\right) \\ $$$$\Rightarrow\Sigma\frac{{a}^{\mathrm{3}} }{\mathrm{4}{a}+{b}+{c}}\geqslant\Sigma\left(\frac{{a}^{\mathrm{2}} }{\mathrm{3}}\right)−\Sigma\frac{{a}\left(\mathrm{4}{a}+{b}+{c}\right)}{\mathrm{36}}\geqslant\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{3}}−\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$

Commented by York12 last updated on 04/Nov/23

Good JOB !

$$\mathrm{Good}\:\mathrm{JOB}\:! \\ $$

Commented by hardmath last updated on 05/Nov/23

thank you ser

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{ser} \\ $$

Answered by York12 last updated on 04/Nov/23

WLOG :a+b+c=3 ⇒(a^3 /(4a+b+c))+(b^3 /(4b+a+c))+(c^3 /(4c+a+b))=(a^3 /(3a+3))+(b^3 /(3b+3))+(c^3 /(3c+3)) Assume: (a^3 /(3a+3))≥ma^2 +n ⇔a^3 (1−3m)−3ma^2 −3an−3n≥0 p(a)=a^3 (1−3m)−3ma^2 −3an−3n p′(a)=3a^2 (1−3m)−6ma−3n p(1)=1−(6m+6n)=0 ⇒m+n=(1/6) p′(1)=3−15m−3n⇒5m+n=1 ⇒m=(5/(24)) and n=((−1)/(24)) ⇒p(a)=(1/(24))((a−1)^2 (3a+1))≥0 ∀ a ∈ R^+ ⇒Σ_(cyc) ((a^3 /(4a+b+c)))≥((5(a^2 +b^2 +c^2 )−3)/(24)) We have (a+b+c)^2 =9≤3(a^2 +b^2 +c^2 ) ⇒(a^2 +b^2 +c^2 )≥3 ⇒Σ_(cyc) ((a^3 /(4a+b+c)))≥((5(a^2 +b^2 +c^2 )−3)/(24))≥((4(a^2 +b^2 +c^2 )−3+3)/(24))=((a^2 +b^2 +c^2 )/6) (Hence proved)

$$\mathrm{WLOG}\::{a}+{b}+{c}=\mathrm{3}\: \\ $$$$\Rightarrow\frac{{a}^{\mathrm{3}} }{\mathrm{4}{a}+{b}+{c}}+\frac{{b}^{\mathrm{3}} }{\mathrm{4}{b}+{a}+{c}}+\frac{{c}^{\mathrm{3}} }{\mathrm{4}{c}+{a}+{b}}=\frac{{a}^{\mathrm{3}} }{\mathrm{3}{a}+\mathrm{3}}+\frac{{b}^{\mathrm{3}} }{\mathrm{3}{b}+\mathrm{3}}+\frac{{c}^{\mathrm{3}} }{\mathrm{3}{c}+\mathrm{3}} \\ $$$$\mathrm{Assume}:\:\frac{{a}^{\mathrm{3}} }{\mathrm{3}{a}+\mathrm{3}}\geqslant{ma}^{\mathrm{2}} +{n}\:\Leftrightarrow{a}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{3}{m}\right)−\mathrm{3}{ma}^{\mathrm{2}} −\mathrm{3}{an}−\mathrm{3}{n}\geqslant\mathrm{0} \\ $$$$\mathrm{p}\left(\mathrm{a}\right)={a}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{3}{m}\right)−\mathrm{3}{ma}^{\mathrm{2}} −\mathrm{3}{an}−\mathrm{3}{n} \\ $$$$\mathrm{p}'\left(\mathrm{a}\right)=\mathrm{3}{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{m}\right)−\mathrm{6}{ma}−\mathrm{3}{n} \\ $$$${p}\left(\mathrm{1}\right)=\mathrm{1}−\left(\mathrm{6}{m}+\mathrm{6}{n}\right)=\mathrm{0}\:\Rightarrow{m}+{n}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${p}'\left(\mathrm{1}\right)=\mathrm{3}−\mathrm{15m}−\mathrm{3n}\Rightarrow\mathrm{5}{m}+{n}=\mathrm{1} \\ $$$$\Rightarrow{m}=\frac{\mathrm{5}}{\mathrm{24}}\:{and}\:\:{n}=\frac{−\mathrm{1}}{\mathrm{24}}\: \\ $$$$\Rightarrow\mathrm{p}\left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{24}}\left(\left({a}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{3}{a}+\mathrm{1}\right)\right)\geqslant\mathrm{0}\:\:\forall\:{a}\:\in\:\mathbb{R}^{+} \\ $$$$\Rightarrow\underset{\mathrm{cyc}} {\sum}\left(\frac{{a}^{\mathrm{3}} }{\mathrm{4}{a}+{b}+{c}}\right)\geqslant\frac{\mathrm{5}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\mathrm{3}}{\mathrm{24}} \\ $$$${W}\mathrm{e}\:\mathrm{have}\:\left({a}+{b}+{c}\right)^{\mathrm{2}} =\mathrm{9}\leqslant\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\geqslant\mathrm{3} \\ $$$$\Rightarrow\underset{\mathrm{cyc}} {\sum}\left(\frac{{a}^{\mathrm{3}} }{\mathrm{4}{a}+{b}+{c}}\right)\geqslant\frac{\mathrm{5}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\mathrm{3}}{\mathrm{24}}\geqslant\frac{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\mathrm{3}+\mathrm{3}}{\mathrm{24}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\left({H}\mathrm{ence}\:\mathrm{proved}\right) \\ $$$$ \\ $$

Commented by hardmath last updated on 05/Nov/23

thank you ser

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{ser} \\ $$

Commented by York12 last updated on 05/Nov/23

ur welcome

$$\mathrm{ur}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com