Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 199101 by cortano12 last updated on 28/Oct/23

Answered by ajfour last updated on 28/Oct/23

Commented by ajfour last updated on 28/Oct/23

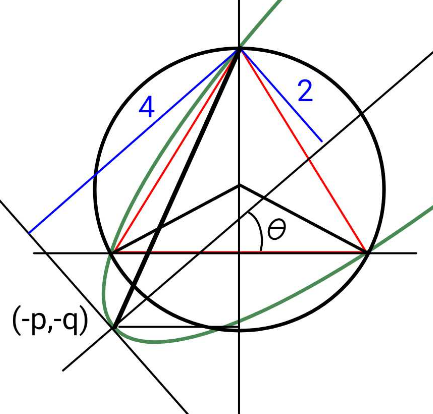
Triangle side be 2(√3)s. Rcos 30°=s(√3) ⇒ R=2 Centre C(0,1) x^2 +(y−1)^2 =4 If M be bottom end of blue line, then M(−4cos θ, 3−4sin θ) p^2 +(3+q)^2 =20 −p=−4cos θ+2sin θ −q=3−4sin θ−2cos θ paeabola axis y+q=((sin θ)/(cos θ))(x+p) for y=0 , x_A =((qcos θ)/(sin θ))−p Line through (−p,−q) ⊥ to axis y+q+((cos θ)/(sin θ))(x+p)=0 for y=0 x_D =−p−((qsin θ)/(cos θ)) now (∓s(√3)−x_D )cos θ=(x_A ±s(√3))^2 sin^2 θ say ±s(√3) =t (t+p+((qsin θ)/(cos θ)))cos θ=(((qcos θ)/(sin θ))−p−t)^2 sin^2 θ sum of roots=0 ⇒ cos θ=2sin θ(psin θ−qcos θ) ⇒ cos θ=2sin θ{3cos θ−4sin θcos θ−2cos^2 θ +4sin θcos θ−2sin^2 θ} ⇒ cos θ=2sin θ(3cos θ−2) cos^2 θ=4(1−cos^2 θ)(3cos θ−2)^2 z^2 =4(1−z^2 )(3z−2)^2 .....

$${Triangle}\:{side}\:{be}\:\mathrm{2}\sqrt{\mathrm{3}}{s}. \\ $$$${R}\mathrm{cos}\:\mathrm{30}°={s}\sqrt{\mathrm{3}}\:\:\:\Rightarrow\:\:{R}=\mathrm{2} \\ $$$${Centre}\:{C}\left(\mathrm{0},\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$${If}\:{M}\:{be}\:{bottom}\:{end}\:{of}\:{blue}\:\:{line}, \\ $$$${then}\:\:{M}\left(−\mathrm{4cos}\:\theta,\:\mathrm{3}−\mathrm{4sin}\:\theta\right) \\ $$$${p}^{\mathrm{2}} +\left(\mathrm{3}+{q}\right)^{\mathrm{2}} =\mathrm{20} \\ $$$$−{p}=−\mathrm{4cos}\:\theta+\mathrm{2sin}\:\theta \\ $$$$−{q}=\mathrm{3}−\mathrm{4sin}\:\theta−\mathrm{2cos}\:\theta \\ $$$${paeabola}\:{axis} \\ $$$${y}+{q}=\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\left({x}+{p}\right) \\ $$$${for}\:{y}=\mathrm{0}\:\:,\:\:\:{x}_{{A}} =\frac{{q}\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}−{p} \\ $$$${Line}\:{through}\:\left(−{p},−{q}\right)\:\bot\:{to}\:{axis} \\ $$$${y}+{q}+\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\left({x}+{p}\right)=\mathrm{0}\:\:\: \\ $$$${for}\:{y}=\mathrm{0}\:\:\:{x}_{{D}} =−{p}−\frac{{q}\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$${now}\:\:\:\left(\mp{s}\sqrt{\mathrm{3}}−{x}_{{D}} \right)\mathrm{cos}\:\theta=\left({x}_{{A}} \pm{s}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${say}\:\:\pm{s}\sqrt{\mathrm{3}}\:={t} \\ $$$$\left({t}+{p}+\frac{{q}\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\right)\mathrm{cos}\:\theta=\left(\frac{{q}\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}−{p}−{t}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${sum}\:{of}\:{roots}=\mathrm{0}\:\:\Rightarrow \\ $$$$\mathrm{cos}\:\theta=\mathrm{2sin}\:\theta\left({p}\mathrm{sin}\:\theta−{q}\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta=\mathrm{2sin}\:\theta\left\{\mathrm{3cos}\:\theta−\mathrm{4sin}\:\theta\mathrm{cos}\:\theta−\mathrm{2cos}\:^{\mathrm{2}} \theta\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4sin}\:\theta\mathrm{cos}\:\theta−\mathrm{2sin}\:^{\mathrm{2}} \theta\right\} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\theta=\mathrm{2sin}\:\theta\left(\mathrm{3cos}\:\theta−\mathrm{2}\right) \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{4}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)\left(\mathrm{3cos}\:\theta−\mathrm{2}\right)^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−{z}^{\mathrm{2}} \right)\left(\mathrm{3}{z}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$..... \\ $$$$ \\ $$

Answered by mr W last updated on 28/Oct/23

y=x^2 line 1: y=4+(x−2)tan α line 2: y=4+(x−2)tan (α+(π/3)) with m_1 =tan α=k m_2 =tan (α+(π/3))=((k+(√3))/(1−(√3)k)) intersection line 1: y_1 =x_1 ^2 =4+(x_1 −2) m_1 ⇒x_1 ^2 −m_1 x_1 +2m_1 −4=0 ⇒x_1 =m_1 −2 intersection line 2: y_2 =x_2 ^2 =4+(x_2 −2) m_2 ⇒x_2 =m_2 −2 s^2 =(x_1 −2)^2 +(y_1 −4)^2 =(m_1 −4)^2 (m_1 ^2 +1) s^2 =(x_2 −2)^2 +(y_2 −4)^2 =(m_2 −4)^2 (m_2 ^2 +1) (m_1 −4)^2 (m_1 ^2 +1)=(m_2 −4)^2 (m_2 ^2 +1) we get 4 roots. they show 2 suitable solutions.

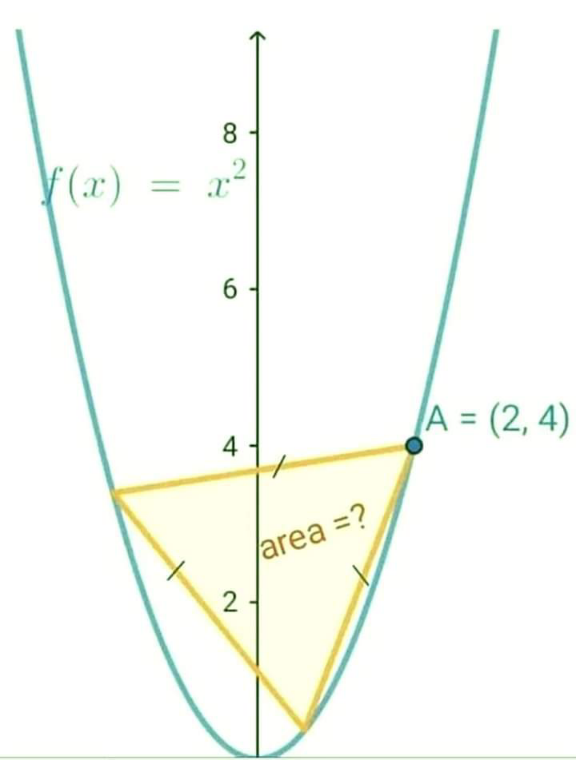
$${y}={x}^{\mathrm{2}} \\ $$$${line}\:\mathrm{1}:\:{y}=\mathrm{4}+\left({x}−\mathrm{2}\right)\mathrm{tan}\:\alpha \\ $$$${line}\:\mathrm{2}:\:{y}=\mathrm{4}+\left({x}−\mathrm{2}\right)\mathrm{tan}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right) \\ $$$${with}\:{m}_{\mathrm{1}} =\mathrm{tan}\:\alpha={k} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{m}_{\mathrm{2}} =\mathrm{tan}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)=\frac{{k}+\sqrt{\mathrm{3}}}{\mathrm{1}−\sqrt{\mathrm{3}}{k}} \\ $$$${intersection}\:{line}\:\mathrm{1}: \\ $$$${y}_{\mathrm{1}} ={x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4}+\left({x}_{\mathrm{1}} −\mathrm{2}\right)\:{m}_{\mathrm{1}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} ^{\mathrm{2}} −{m}_{\mathrm{1}} {x}_{\mathrm{1}} +\mathrm{2}{m}_{\mathrm{1}} −\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1}} ={m}_{\mathrm{1}} −\mathrm{2} \\ $$$${intersection}\:{line}\:\mathrm{2}: \\ $$$${y}_{\mathrm{2}} ={x}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{4}+\left({x}_{\mathrm{2}} −\mathrm{2}\right)\:{m}_{\mathrm{2}} \\ $$$$\Rightarrow{x}_{\mathrm{2}} ={m}_{\mathrm{2}} −\mathrm{2} \\ $$$$ \\ $$$${s}^{\mathrm{2}} =\left({x}_{\mathrm{1}} −\mathrm{2}\right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} −\mathrm{4}\right)^{\mathrm{2}} =\left({m}_{\mathrm{1}} −\mathrm{4}\right)^{\mathrm{2}} \left({m}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${s}^{\mathrm{2}} =\left({x}_{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} +\left({y}_{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} =\left({m}_{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \left({m}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\left({m}_{\mathrm{1}} −\mathrm{4}\right)^{\mathrm{2}} \left({m}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}\right)=\left({m}_{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \left({m}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${we}\:{get}\:\mathrm{4}\:{roots}.\:{they}\:{show}\:\mathrm{2}\:{suitable}\: \\ $$$${solutions}. \\ $$

Commented by mr W last updated on 28/Oct/23

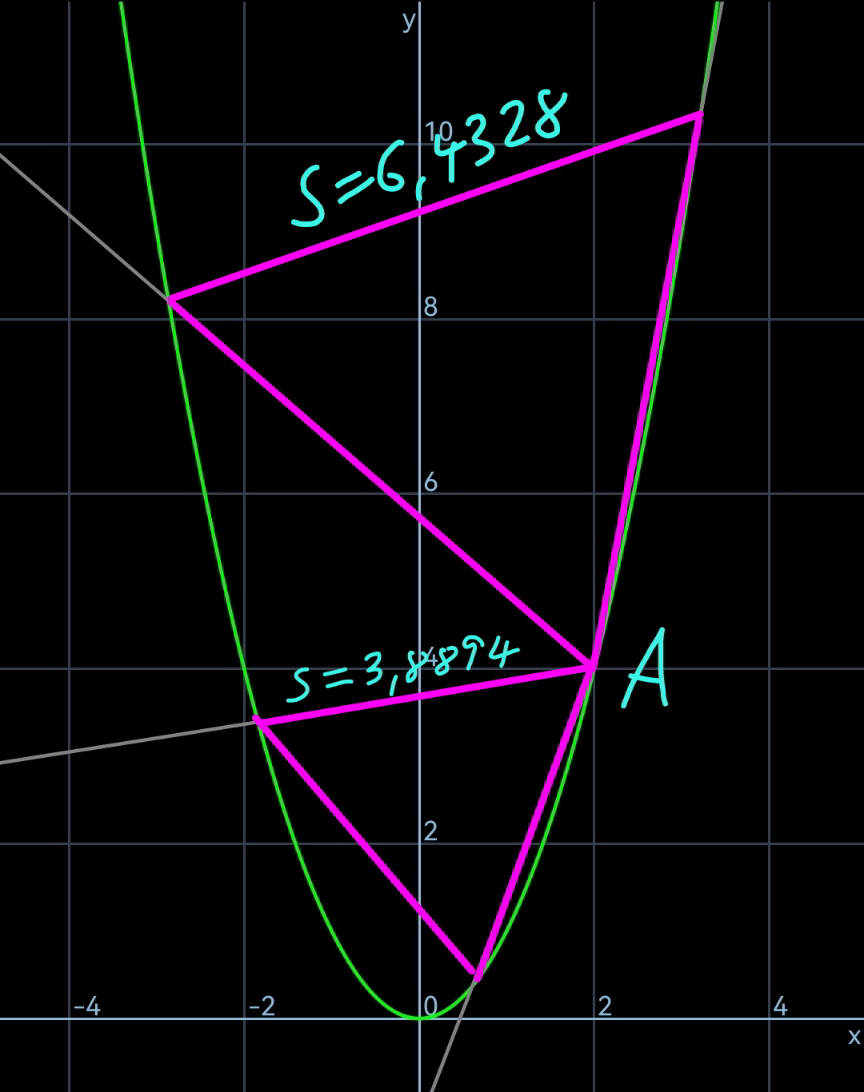
Commented by cortano12 last updated on 28/Oct/23

great sir

$$\mathrm{great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 28/Oct/23

Alternative method: acc. to the solution from ajfour sir in Q62938, for a given side length s of the equilateral triangle, its vertexes satisfy following equation: x^3 −3hx^2 +px+q=0 with h=((√(s^2 −12))/(4(√3))), k= ((3s^2 )/(16))−(1/4), p=((9h^2 −3k)/2), q=((h^2 +k^2 −s^2 /3)/(3h)) now it is given x=2, reversely we can get s.

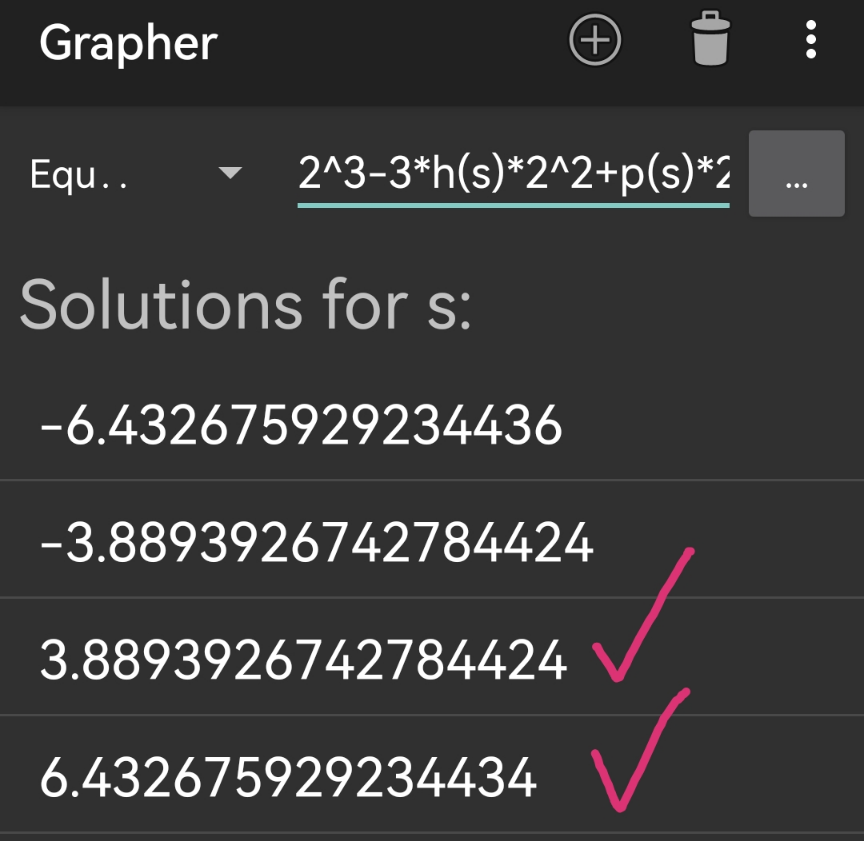
$$\underline{{Alternative}\:{method}:} \\ $$$${acc}.\:{to}\:{the}\:{solution}\:{from}\:\boldsymbol{{ajfour}}\:{sir} \\ $$$${in}\:{Q}\mathrm{62938},\:{for}\:{a}\:{given}\:{side}\:{length}\:\boldsymbol{{s}}\: \\ $$$${of}\:{the}\:{equilateral}\:{triangle},\:{its}\: \\ $$$${vertexes}\:{satisfy}\:{following}\:{equation}: \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{hx}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\: \\ $$$${with}\:{h}=\frac{\sqrt{\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{12}}}{\mathrm{4}\sqrt{\mathrm{3}}},\:{k}=\:\frac{\mathrm{3}\boldsymbol{{s}}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}}, \\ $$$${p}=\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}},\:{q}=\frac{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} −\boldsymbol{{s}}^{\mathrm{2}} /\mathrm{3}}{\mathrm{3}{h}} \\ $$$${now}\:{it}\:{is}\:{given}\:{x}=\mathrm{2},\:{reversely}\:{we} \\ $$$${can}\:{get}\:{s}. \\ $$

Commented by mr W last updated on 28/Oct/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com