Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199015 by Tawa11 last updated on 26/Oct/23

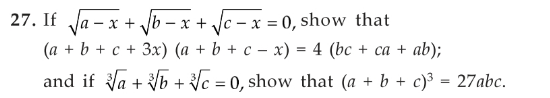
Answered by Rasheed.Sindhi last updated on 26/Oct/23

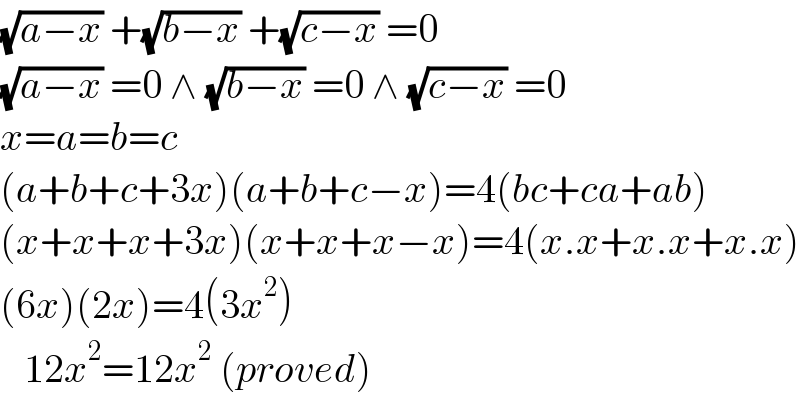
(√(a−x)) +(√(b−x)) +(√(c−x)) =0 (√(a−x)) =0 ∧ (√(b−x)) =0 ∧ (√(c−x)) =0 x=a=b=c (a+b+c+3x)(a+b+c−x)=4(bc+ca+ab) (x+x+x+3x)(x+x+x−x)=4(x.x+x.x+x.x) (6x)(2x)=4(3x^2 ) 12x^2 =12x^2 (proved)

$$\sqrt{{a}−{x}}\:+\sqrt{{b}−{x}}\:+\sqrt{{c}−{x}}\:=\mathrm{0} \\ $$$$\sqrt{{a}−{x}}\:=\mathrm{0}\:\wedge\:\sqrt{{b}−{x}}\:=\mathrm{0}\:\wedge\:\sqrt{{c}−{x}}\:=\mathrm{0} \\ $$$${x}={a}={b}={c} \\ $$$$\left({a}+{b}+{c}+\mathrm{3}{x}\right)\left({a}+{b}+{c}−{x}\right)=\mathrm{4}\left({bc}+{ca}+{ab}\right) \\ $$$$\left({x}+{x}+{x}+\mathrm{3}{x}\right)\left({x}+{x}+{x}−{x}\right)=\mathrm{4}\left({x}.{x}+{x}.{x}+{x}.{x}\right) \\ $$$$\left(\mathrm{6}{x}\right)\left(\mathrm{2}{x}\right)=\mathrm{4}\left(\mathrm{3}{x}^{\mathrm{2}} \right) \\ $$$$\:\:\:\mathrm{12}{x}^{\mathrm{2}} =\mathrm{12}{x}^{\mathrm{2}} \:\left({proved}\right) \\ $$

Commented by Tawa11 last updated on 26/Oct/23

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by Rasheed.Sindhi last updated on 26/Oct/23

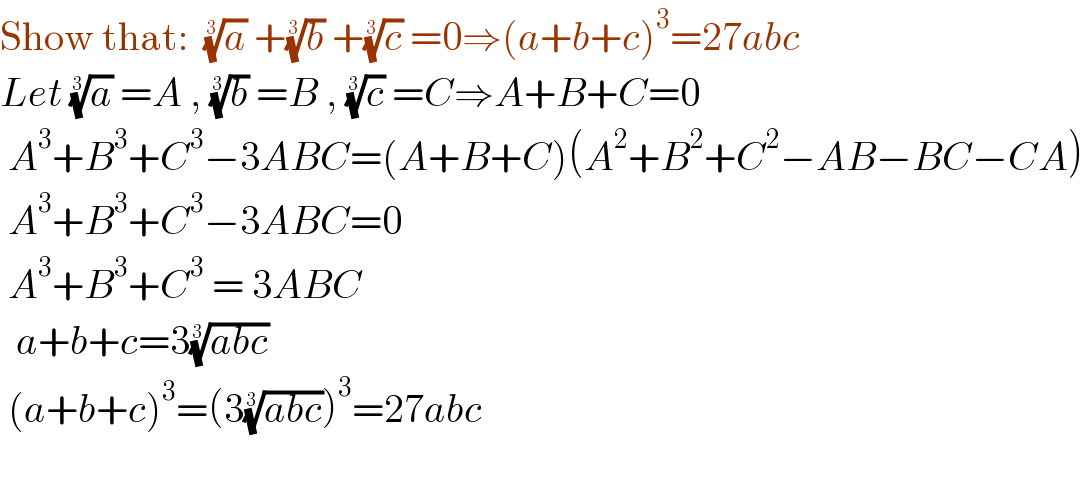
Show that: (a)^(1/3) +(b)^(1/3) +(c)^(1/3) =0⇒(a+b+c)^3 =27abc Let (a)^(1/3) =A , (b)^(1/3) =B , (c)^(1/3) =C⇒A+B+C=0 A^3 +B^3 +C^3 −3ABC=(A+B+C)(A^2 +B^2 +C^2 −AB−BC−CA) A^3 +B^3 +C^3 −3ABC=0 A^3 +B^3 +C^3 = 3ABC a+b+c=3((abc))^(1/3) (a+b+c)^3 =(3((abc))^(1/3) )^3 =27abc

$$\mathrm{Show}\:\mathrm{that}:\:\:\sqrt[{\mathrm{3}}]{{a}}\:+\sqrt[{\mathrm{3}}]{{b}}\:+\sqrt[{\mathrm{3}}]{{c}}\:=\mathrm{0}\Rightarrow\left({a}+{b}+{c}\right)^{\mathrm{3}} =\mathrm{27}{abc} \\ $$$${Let}\:\sqrt[{\mathrm{3}}]{{a}}\:={A}\:,\:\sqrt[{\mathrm{3}}]{{b}}\:={B}\:,\:\sqrt[{\mathrm{3}}]{{c}}\:={C}\Rightarrow{A}+{B}+{C}=\mathrm{0} \\ $$$$\:{A}^{\mathrm{3}} +{B}^{\mathrm{3}} +{C}^{\mathrm{3}} −\mathrm{3}{ABC}=\left({A}+{B}+{C}\right)\left({A}^{\mathrm{2}} +{B}^{\mathrm{2}} +{C}^{\mathrm{2}} −{AB}−{BC}−{CA}\right) \\ $$$$\:{A}^{\mathrm{3}} +{B}^{\mathrm{3}} +{C}^{\mathrm{3}} −\mathrm{3}{ABC}=\mathrm{0} \\ $$$$\:{A}^{\mathrm{3}} +{B}^{\mathrm{3}} +{C}^{\mathrm{3}} \:=\:\mathrm{3}{ABC} \\ $$$$\:\:{a}+{b}+{c}=\mathrm{3}\sqrt[{\mathrm{3}}]{{abc}}\: \\ $$$$\:\left({a}+{b}+{c}\right)^{\mathrm{3}} =\left(\mathrm{3}\sqrt[{\mathrm{3}}]{{abc}}\right)^{\mathrm{3}} =\mathrm{27}{abc} \\ $$$$\:\:\: \\ $$

Commented by Tawa11 last updated on 26/Oct/23

God bless you sir. Thanks for your time.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com