Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 198785 by sonukgindia last updated on 24/Oct/23

Answered by deleteduser1 last updated on 24/Oct/23

(1/(197))≡x(mod 3000)⇒197x≡1(mod 3000) 197x≡1(mod 3)⇒−x≡^3 1⇒x≡^3 2 197x≡1(mod 8)⇒5x≡1(mod 8)⇒x≡^8 5 197x≡1(mod 125)⇒72x≡1(mod 125) ⇒−53x≡1(mod 125)⇒[3x≡^(25) −1⇒x≡^(25) 8] 53x≡^(125) 124+125×13⇒x≡33(mod 125) x=3k+2;x=8q+5⇒8q+5≡2(mod 3) ⇒q≡0(mod 3)⇒x=24v+5≡33(mod 125) ⇒24v≡28(mod 125)⇒6v≡^(125) 7⇒v≡22(mod 125) ⇒x=24(125y+22)+5⇒x≡24×22+5=533 ⇒x≡533(mod 3000)

$$\frac{\mathrm{1}}{\mathrm{197}}\equiv{x}\left({mod}\:\mathrm{3000}\right)\Rightarrow\mathrm{197}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{3000}\right) \\ $$$$\mathrm{197}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{3}\right)\Rightarrow−{x}\overset{\mathrm{3}} {\equiv}\mathrm{1}\Rightarrow{x}\overset{\mathrm{3}} {\equiv}\mathrm{2} \\ $$$$\mathrm{197}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{8}\right)\Rightarrow\mathrm{5}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{8}\right)\Rightarrow{x}\overset{\mathrm{8}} {\equiv}\mathrm{5} \\ $$$$\mathrm{197}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{125}\right)\Rightarrow\mathrm{72}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{125}\right) \\ $$$$\Rightarrow−\mathrm{53}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{125}\right)\Rightarrow\left[\mathrm{3}{x}\overset{\mathrm{25}} {\equiv}−\mathrm{1}\Rightarrow{x}\overset{\mathrm{25}} {\equiv}\mathrm{8}\right] \\ $$$$\mathrm{53}{x}\overset{\mathrm{125}} {\equiv}\mathrm{124}+\mathrm{125}×\mathrm{13}\Rightarrow{x}\equiv\mathrm{33}\left({mod}\:\mathrm{125}\right) \\ $$$${x}=\mathrm{3}{k}+\mathrm{2};{x}=\mathrm{8}{q}+\mathrm{5}\Rightarrow\mathrm{8}{q}+\mathrm{5}\equiv\mathrm{2}\left({mod}\:\mathrm{3}\right) \\ $$$$\Rightarrow{q}\equiv\mathrm{0}\left({mod}\:\mathrm{3}\right)\Rightarrow{x}=\mathrm{24}{v}+\mathrm{5}\equiv\mathrm{33}\left({mod}\:\mathrm{125}\right) \\ $$$$\Rightarrow\mathrm{24}{v}\equiv\mathrm{28}\left({mod}\:\mathrm{125}\right)\Rightarrow\mathrm{6}{v}\overset{\mathrm{125}} {\equiv}\mathrm{7}\Rightarrow{v}\equiv\mathrm{22}\left({mod}\:\mathrm{125}\right) \\ $$$$\Rightarrow{x}=\mathrm{24}\left(\mathrm{125}{y}+\mathrm{22}\right)+\mathrm{5}\Rightarrow{x}\equiv\mathrm{24}×\mathrm{22}+\mathrm{5}=\mathrm{533} \\ $$$$\Rightarrow{x}\equiv\mathrm{533}\left({mod}\:\mathrm{3000}\right) \\ $$

Commented by qaz last updated on 24/Oct/23

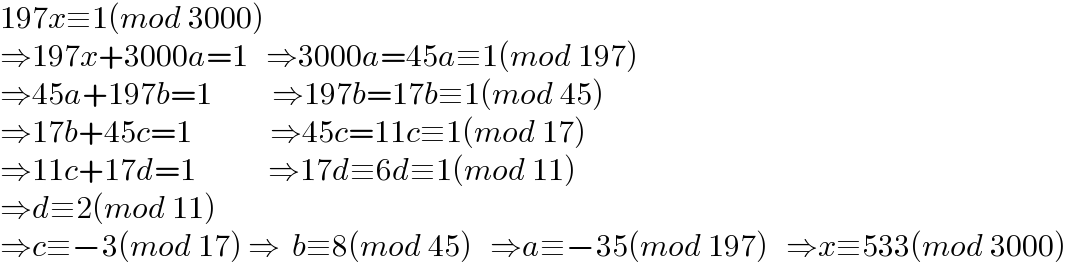
197x≡1(mod 3000) ⇒197x+3000a=1 ⇒3000a=45a≡1(mod 197) ⇒45a+197b=1 ⇒197b=17b≡1(mod 45) ⇒17b+45c=1 ⇒45c=11c≡1(mod 17) ⇒11c+17d=1 ⇒17d≡6d≡1(mod 11) ⇒d≡2(mod 11) ⇒c≡−3(mod 17) ⇒ b≡8(mod 45) ⇒a≡−35(mod 197) ⇒x≡533(mod 3000)

$$\mathrm{197}{x}\equiv\mathrm{1}\left({mod}\:\mathrm{3000}\right) \\ $$$$\Rightarrow\mathrm{197}{x}+\mathrm{3000}{a}=\mathrm{1}\:\:\:\Rightarrow\mathrm{3000}{a}=\mathrm{45}{a}\equiv\mathrm{1}\left({mod}\:\mathrm{197}\right) \\ $$$$\Rightarrow\mathrm{45}{a}+\mathrm{197}{b}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{197}{b}=\mathrm{17}{b}\equiv\mathrm{1}\left({mod}\:\mathrm{45}\right) \\ $$$$\Rightarrow\mathrm{17}{b}+\mathrm{45}{c}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{45}{c}=\mathrm{11}{c}\equiv\mathrm{1}\left({mod}\:\mathrm{17}\right) \\ $$$$\Rightarrow\mathrm{11}{c}+\mathrm{17}{d}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{17}{d}\equiv\mathrm{6}{d}\equiv\mathrm{1}\left({mod}\:\mathrm{11}\right) \\ $$$$\Rightarrow{d}\equiv\mathrm{2}\left({mod}\:\mathrm{11}\right) \\ $$$$\Rightarrow{c}\equiv−\mathrm{3}\left({mod}\:\mathrm{17}\right)\:\Rightarrow\:\:{b}\equiv\mathrm{8}\left({mod}\:\mathrm{45}\right)\:\:\:\Rightarrow{a}\equiv−\mathrm{35}\left({mod}\:\mathrm{197}\right)\:\:\:\Rightarrow{x}\equiv\mathrm{533}\left({mod}\:\mathrm{3000}\right) \\ $$

Answered by deleteduser1 last updated on 24/Oct/23

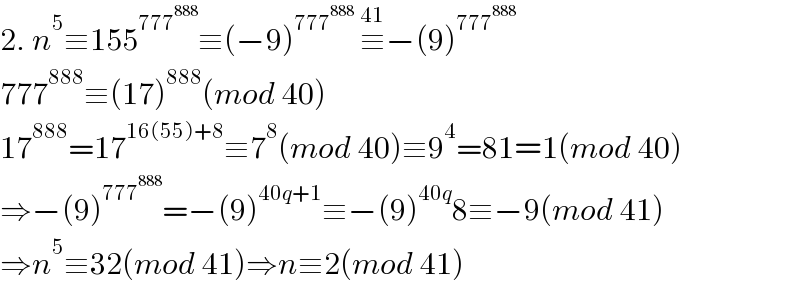
2. n^5 ≡155^(777^(888) ) ≡(−9)^(777^(888) ) ≡^(41) −(9)^(777^(888) ) 777^(888) ≡(17)^(888) (mod 40) 17^(888) =17^(16(55)+8) ≡7^8 (mod 40)≡9^4 =81=1(mod 40) ⇒−(9)^(777^(888) ) =−(9)^(40q+1) ≡−(9)^(40q) 8≡−9(mod 41) ⇒n^5 ≡32(mod 41)⇒n≡2(mod 41)

$$\mathrm{2}.\:{n}^{\mathrm{5}} \equiv\mathrm{155}^{\mathrm{777}^{\mathrm{888}} } \equiv\left(−\mathrm{9}\right)^{\mathrm{777}^{\mathrm{888}} } \:\overset{\mathrm{41}} {\equiv}−\left(\mathrm{9}\right)^{\mathrm{777}^{\mathrm{888}} } \\ $$$$\mathrm{777}^{\mathrm{888}} \equiv\left(\mathrm{17}\right)^{\mathrm{888}} \left({mod}\:\mathrm{40}\right) \\ $$$$\mathrm{17}^{\mathrm{888}} =\mathrm{17}^{\mathrm{16}\left(\mathrm{55}\right)+\mathrm{8}} \equiv\mathrm{7}^{\mathrm{8}} \left({mod}\:\mathrm{40}\right)\equiv\mathrm{9}^{\mathrm{4}} =\mathrm{81}=\mathrm{1}\left({mod}\:\mathrm{40}\right) \\ $$$$\Rightarrow−\left(\mathrm{9}\right)^{\mathrm{777}^{\mathrm{888}} } =−\left(\mathrm{9}\right)^{\mathrm{40}{q}+\mathrm{1}} \equiv−\left(\mathrm{9}\right)^{\mathrm{40}{q}} \mathrm{8}\equiv−\mathrm{9}\left({mod}\:\mathrm{41}\right) \\ $$$$\Rightarrow{n}^{\mathrm{5}} \equiv\mathrm{32}\left({mod}\:\mathrm{41}\right)\Rightarrow{n}\equiv\mathrm{2}\left({mod}\:\mathrm{41}\right) \\ $$

Answered by deleteduser1 last updated on 24/Oct/23

3. n^5 ≡6^k (mod 41)⇒6^(5q) ≡6^k (mod 41) 6^(5q−k) ≡6^(40) (mod 41)⇒5q≡k(mod 40) ⇒k≡5q(mod 40)⇒k≡5q(mod 41) where 5q≤40 ⇒x≡6^0 ,6^5 ,6^(10) ,6^(15) ,6^(20) ,6^(25) ,6^(30) ,6^(35) x∈{[1],[3],[9],[14],[27],[32],[38]}

$$\mathrm{3}.\:{n}^{\mathrm{5}} \equiv\mathrm{6}^{{k}} \left({mod}\:\mathrm{41}\right)\Rightarrow\mathrm{6}^{\mathrm{5}{q}} \equiv\mathrm{6}^{{k}} \left({mod}\:\mathrm{41}\right) \\ $$$$\mathrm{6}^{\mathrm{5}{q}−{k}} \equiv\mathrm{6}^{\mathrm{40}} \left({mod}\:\mathrm{41}\right)\Rightarrow\mathrm{5}{q}\equiv{k}\left({mod}\:\mathrm{40}\right) \\ $$$$\Rightarrow{k}\equiv\mathrm{5}{q}\left({mod}\:\mathrm{40}\right)\Rightarrow{k}\equiv\mathrm{5}{q}\left({mod}\:\mathrm{41}\right)\:{where}\:\mathrm{5}{q}\leqslant\mathrm{40} \\ $$$$\Rightarrow{x}\equiv\mathrm{6}^{\mathrm{0}} ,\mathrm{6}^{\mathrm{5}} ,\mathrm{6}^{\mathrm{10}} ,\mathrm{6}^{\mathrm{15}} ,\mathrm{6}^{\mathrm{20}} ,\mathrm{6}^{\mathrm{25}} ,\mathrm{6}^{\mathrm{30}} ,\mathrm{6}^{\mathrm{35}} \\ $$$${x}\in\left\{\left[\mathrm{1}\right],\left[\mathrm{3}\right],\left[\mathrm{9}\right],\left[\mathrm{14}\right],\left[\mathrm{27}\right],\left[\mathrm{32}\right],\left[\mathrm{38}\right]\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com