Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 198489 by sonukgindia last updated on 21/Oct/23

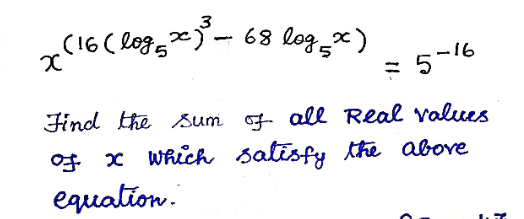
Answered by cortano12 last updated on 21/Oct/23

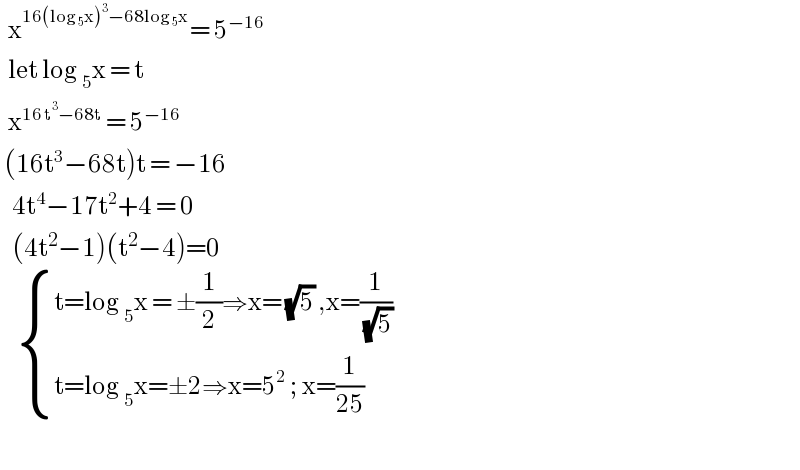
x^(16(log _5 x)^3 −68log _5 x ) = 5^(−16) let log _5 x = t x^(16 t^3 −68t) = 5^(−16) (16t^3 −68t)t = −16 4t^4 −17t^2 +4 = 0 (4t^2 −1)(t^2 −4)=0 { ((t=log _5 x = ±(1/2)⇒x= (√5) ,x=(1/( (√5))))),((t=log _5 x=±2⇒x=5^2 ; x=(1/(25)))) :}

$$\:\:\mathrm{x}^{\mathrm{16}\left(\mathrm{log}\:_{\mathrm{5}} \mathrm{x}\right)^{\mathrm{3}} −\mathrm{68log}\:_{\mathrm{5}} \mathrm{x}\:} =\:\mathrm{5}^{−\mathrm{16}} \\ $$$$\:\:\mathrm{let}\:\mathrm{log}\:_{\mathrm{5}} \mathrm{x}\:=\:\mathrm{t} \\ $$$$\:\:\mathrm{x}^{\mathrm{16}\:\mathrm{t}^{\mathrm{3}} −\mathrm{68t}} \:=\:\mathrm{5}^{−\mathrm{16}} \\ $$$$\:\left(\mathrm{16t}^{\mathrm{3}} −\mathrm{68t}\right)\mathrm{t}\:=\:−\mathrm{16}\: \\ $$$$\:\:\:\mathrm{4t}^{\mathrm{4}} −\mathrm{17t}^{\mathrm{2}} +\mathrm{4}\:=\:\mathrm{0} \\ $$$$\:\:\:\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{4}\right)=\mathrm{0} \\ $$$$\:\:\:\:\begin{cases}{\mathrm{t}=\mathrm{log}\:_{\mathrm{5}} \mathrm{x}\:=\:\pm\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{x}=\:\sqrt{\mathrm{5}}\:,\mathrm{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}}\\{\mathrm{t}=\mathrm{log}\:_{\mathrm{5}} \mathrm{x}=\pm\mathrm{2}\Rightarrow\mathrm{x}=\mathrm{5}^{\mathrm{2}} \:;\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{25}}}\end{cases} \\ $$$$\:\: \\ $$

Commented by Rasheed.Sindhi last updated on 21/Oct/23

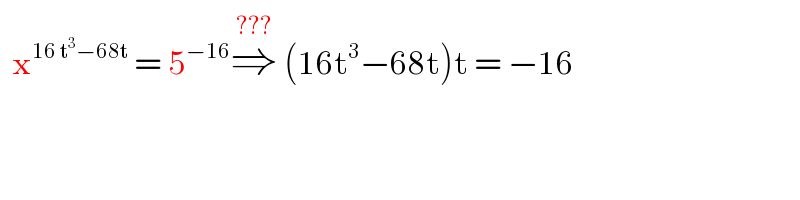
x^(16 t^3 −68t) = 5^(−16) ⇒^(???) (16t^3 −68t)t = −16

$$\:\:\mathrm{x}^{\mathrm{16}\:\mathrm{t}^{\mathrm{3}} −\mathrm{68t}} \:=\:\mathrm{5}^{−\mathrm{16}} \overset{???} {\Rightarrow}\:\left(\mathrm{16t}^{\mathrm{3}} −\mathrm{68t}\right)\mathrm{t}\:=\:−\mathrm{16} \\ $$

Commented by cortano12 last updated on 21/Oct/23

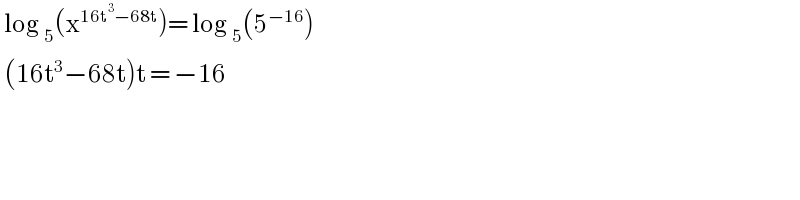
log _5 (x^(16t^3 −68t) )= log _5 (5^(−16) ) (16t^3 −68t)t = −16

$$\:\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{x}^{\mathrm{16t}^{\mathrm{3}} −\mathrm{68t}} \right)=\:\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{5}^{−\mathrm{16}} \right) \\ $$$$\:\left(\mathrm{16t}^{\mathrm{3}} −\mathrm{68t}\right)\mathrm{t}\:=\:−\mathrm{16}\: \\ $$

Commented by Frix last updated on 21/Oct/23

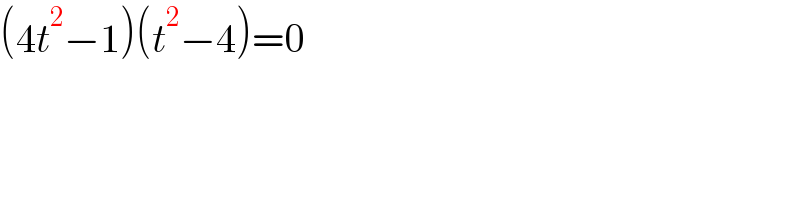
(4t^2 −1)(t^2 −4)=0

$$\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{4}\right)=\mathrm{0} \\ $$

Answered by Frix last updated on 21/Oct/23

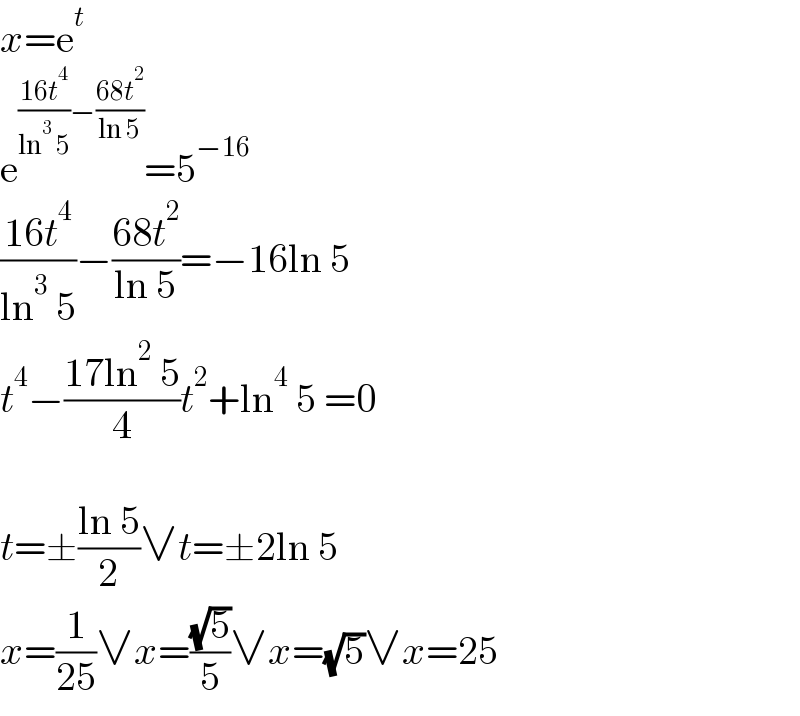
x=e^t e^(((16t^4 )/(ln^3 5))−((68t^2 )/(ln 5))) =5^(−16) ((16t^4 )/(ln^3 5))−((68t^2 )/(ln 5))=−16ln 5 t^4 −((17ln^2 5)/4)t^2 +ln^4 5 =0 t=±((ln 5)/2)∨t=±2ln 5 x=(1/(25))∨x=((√5)/5)∨x=(√5)∨x=25

$${x}=\mathrm{e}^{{t}} \\ $$$$\mathrm{e}^{\frac{\mathrm{16}{t}^{\mathrm{4}} }{\mathrm{ln}^{\mathrm{3}} \:\mathrm{5}}−\frac{\mathrm{68}{t}^{\mathrm{2}} }{\mathrm{ln}\:\mathrm{5}}} =\mathrm{5}^{−\mathrm{16}} \\ $$$$\frac{\mathrm{16}{t}^{\mathrm{4}} }{\mathrm{ln}^{\mathrm{3}} \:\mathrm{5}}−\frac{\mathrm{68}{t}^{\mathrm{2}} }{\mathrm{ln}\:\mathrm{5}}=−\mathrm{16ln}\:\mathrm{5} \\ $$$${t}^{\mathrm{4}} −\frac{\mathrm{17ln}^{\mathrm{2}} \:\mathrm{5}}{\mathrm{4}}{t}^{\mathrm{2}} +\mathrm{ln}^{\mathrm{4}} \:\mathrm{5}\:=\mathrm{0} \\ $$$$ \\ $$$${t}=\pm\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{2}}\vee{t}=\pm\mathrm{2ln}\:\mathrm{5} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{25}}\vee{x}=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\vee{x}=\sqrt{\mathrm{5}}\vee{x}=\mathrm{25} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com