
Question Number 198186 by Tawa11 last updated on 13/Oct/23

Answered by mr W last updated on 13/Oct/23
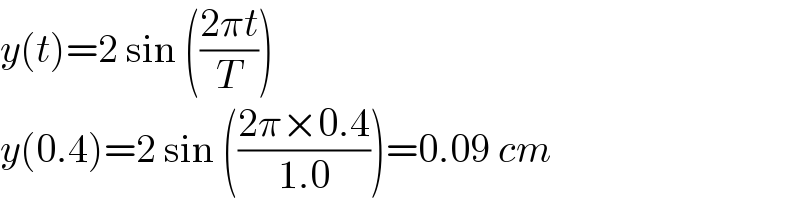
$${y}\left({t}\right)=\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi{t}}{{T}}\right) \\ $$$${y}\left(\mathrm{0}.\mathrm{4}\right)=\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi×\mathrm{0}.\mathrm{4}}{\mathrm{1}.\mathrm{0}}\right)=\mathrm{0}.\mathrm{09}\:{cm} \\ $$
Commented by Tawa11 last updated on 13/Oct/23

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 13/Oct/23
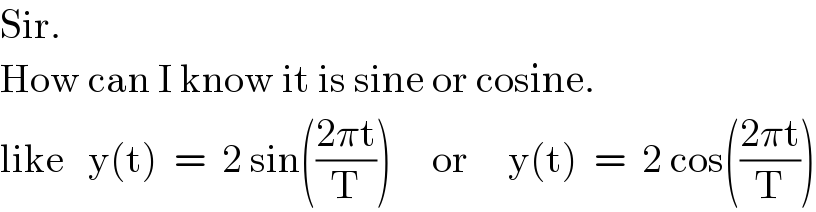
$$\mathrm{Sir}. \\ $$$$\mathrm{How}\:\mathrm{can}\:\mathrm{I}\:\mathrm{know}\:\mathrm{it}\:\mathrm{is}\:\mathrm{sine}\:\mathrm{or}\:\mathrm{cosine}. \\ $$$$\mathrm{like}\:\:\:\mathrm{y}\left(\mathrm{t}\right)\:\:=\:\:\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{2}\pi\mathrm{t}}{\mathrm{T}}\right)\:\:\:\:\:\mathrm{or}\:\:\:\:\:\mathrm{y}\left(\mathrm{t}\right)\:\:=\:\:\mathrm{2}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{t}}{\mathrm{T}}\right) \\ $$
Commented by mr W last updated on 13/Oct/23
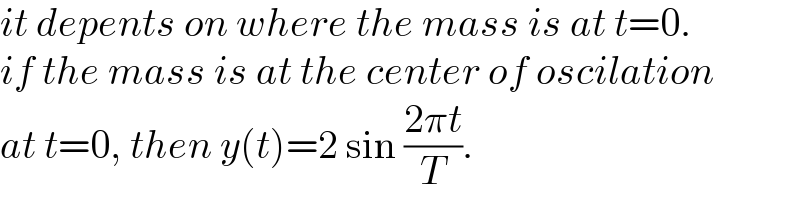
$${it}\:{depents}\:{on}\:{where}\:{the}\:{mass}\:{is}\:{at}\:{t}=\mathrm{0}. \\ $$$${if}\:{the}\:{mass}\:{is}\:{at}\:{the}\:{center}\:{of}\:{oscilation} \\ $$$${at}\:{t}=\mathrm{0},\:{then}\:{y}\left({t}\right)=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{2}\pi{t}}{{T}}. \\ $$
Commented by Tawa11 last updated on 13/Oct/23

$$\mathrm{I}\:\mathrm{appreciate}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
