
Question Number 198050 by akolade last updated on 09/Oct/23
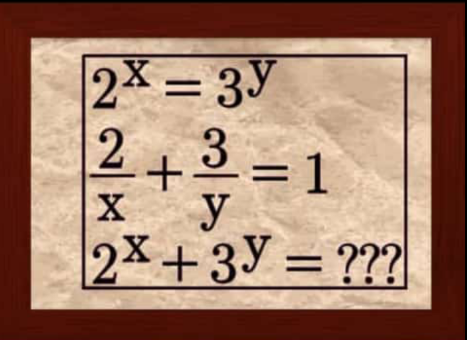
Answered by mr W last updated on 10/Oct/23
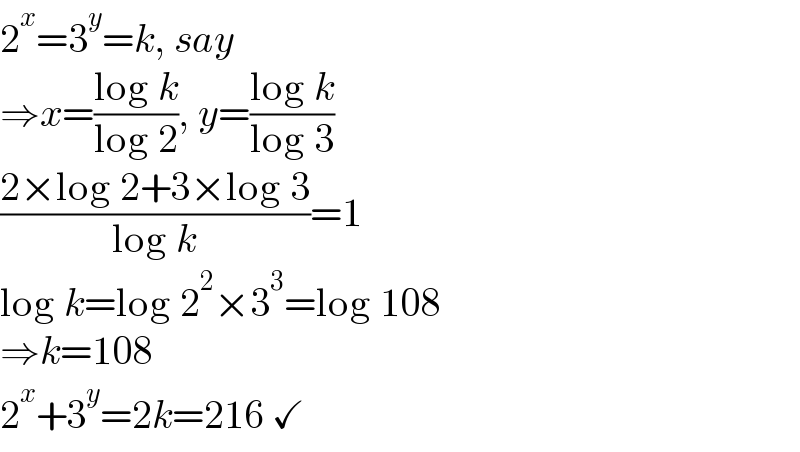
$$\mathrm{2}^{{x}} =\mathrm{3}^{{y}} ={k},\:{say} \\ $$$$\Rightarrow{x}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{2}},\:{y}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{3}} \\ $$$$\frac{\mathrm{2}×\mathrm{log}\:\mathrm{2}+\mathrm{3}×\mathrm{log}\:\mathrm{3}}{\mathrm{log}\:{k}}=\mathrm{1} \\ $$$$\mathrm{log}\:{k}=\mathrm{log}\:\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{3}} =\mathrm{log}\:\mathrm{108} \\ $$$$\Rightarrow{k}=\mathrm{108} \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}^{{y}} =\mathrm{2}{k}=\mathrm{216}\:\checkmark \\ $$
Commented by necx122 last updated on 09/Oct/23
$${My}\:{goodness}.\:{The}\:{approach}\:{is}\:{really} \\ $$$${cool}. \\ $$
Commented by akolade last updated on 10/Oct/23
$$\mathrm{wow}\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{best}\:\mathrm{approach}\:\mathrm{i}\:\mathrm{have}\:\mathrm{seen}\:\mathrm{so}\:\mathrm{far} \\ $$
