
Question Number 197876 by cortano12 last updated on 02/Oct/23

Commented by Frix last updated on 02/Oct/23
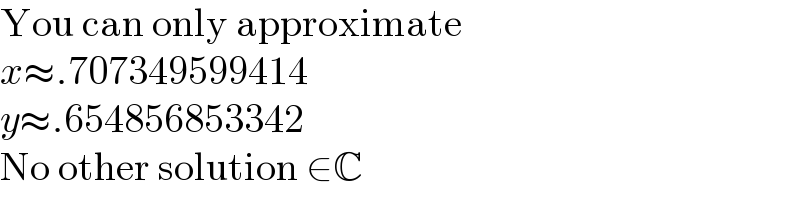
$$\mathrm{You}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate} \\ $$$${x}\approx.\mathrm{707349599414} \\ $$$${y}\approx.\mathrm{654856853342} \\ $$$$\mathrm{No}\:\mathrm{other}\:\mathrm{solution}\:\in\mathbb{C} \\ $$
Answered by mr W last updated on 03/Oct/23
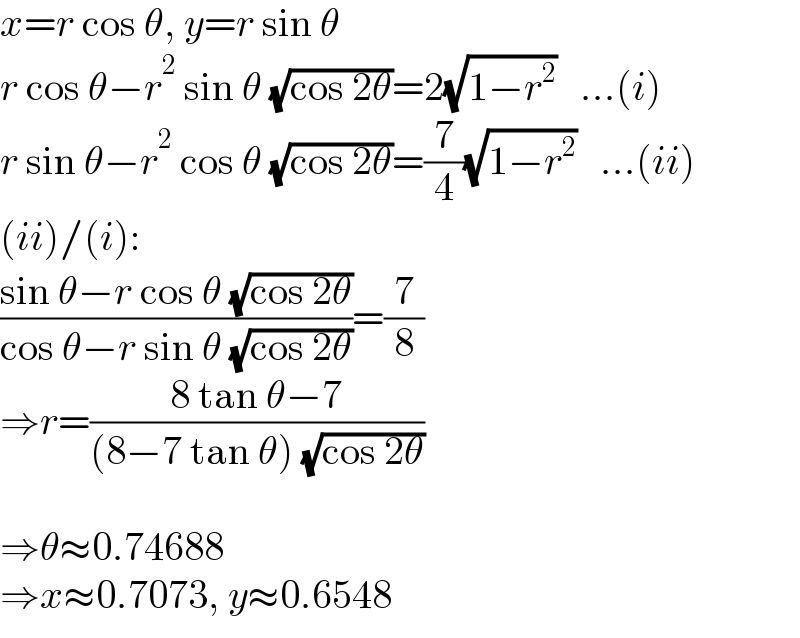
$${x}={r}\:\mathrm{cos}\:\theta,\:{y}={r}\:\mathrm{sin}\:\theta \\ $$$${r}\:\mathrm{cos}\:\theta−{r}^{\mathrm{2}} \:\mathrm{sin}\:\theta\:\sqrt{\mathrm{cos}\:\mathrm{2}\theta}=\mathrm{2}\sqrt{\mathrm{1}−{r}^{\mathrm{2}} }\:\:\:...\left({i}\right) \\ $$$${r}\:\mathrm{sin}\:\theta−{r}^{\mathrm{2}} \:\mathrm{cos}\:\theta\:\sqrt{\mathrm{cos}\:\mathrm{2}\theta}=\frac{\mathrm{7}}{\mathrm{4}}\sqrt{\mathrm{1}−{r}^{\mathrm{2}} }\:\:\:...\left({ii}\right) \\ $$$$\left({ii}\right)/\left({i}\right): \\ $$$$\frac{\mathrm{sin}\:\theta−{r}\:\mathrm{cos}\:\theta\:\sqrt{\mathrm{cos}\:\mathrm{2}\theta}}{\mathrm{cos}\:\theta−{r}\:\mathrm{sin}\:\theta\:\sqrt{\mathrm{cos}\:\mathrm{2}\theta}}=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{8}\:\mathrm{tan}\:\theta−\mathrm{7}}{\left(\mathrm{8}−\mathrm{7}\:\mathrm{tan}\:\theta\right)\:\sqrt{\mathrm{cos}\:\mathrm{2}\theta}} \\ $$$$ \\ $$$$\Rightarrow\theta\approx\mathrm{0}.\mathrm{74688}\: \\ $$$$\Rightarrow{x}\approx\mathrm{0}.\mathrm{7073},\:{y}\approx\mathrm{0}.\mathrm{6548} \\ $$
Commented by cherokeesay last updated on 04/Oct/23

$${thank}\:{you}\:! \\ $$
Answered by Frix last updated on 03/Oct/23
![(√(x^2 −y^2 ))≥0∧(√(1−x^2 −y^2 ))>0 Let p=(√(x^2 −y^2 ))∧q=(√(1−x^2 −y^2 )) ((x−py)/q)=2∧((y−px)/q)=(7/4) ⇔ x=(((7p+8)q)/(4(1−p^2 )))∧y=(((8p+7)q)/(4(1−p^2 ))) ⇒ x−y=(q/(4(1+p^2 )))>0 ⇒ x>y [★] ((x−y(√(x^2 −y^2 )))/( (√(1−x^2 −y^2 ))))=2∧((y−x(√(x^2 −y^2 )))/( (√(1−x^2 −y^2 ))))=(7/4) ⇔ (√(1−x^2 −y^2 ))=((x−y(√(x^2 −y^2 )))/2)=((4(y−x(√(x^2 −y^2 ))))/7) ⇒ (√(x^2 −y^2 ))=((8y−7x)/(8x−7y)) [★] Let x=u(1+v)∧y=u(1−v)∧u>0∧v>0 2∣u∣(√v)=((1−15v)/(1+15v)) ⇒ 0<v≤(1/(15)) u=((1−15v)/(2(√v)(1+15v))) Insert in the following equation & transform x−y(√(x^2 −y^2 ))=2(√(1−x^2 −y^2 )) ⇒ 16v(1−15v)=(1+15v)(√(−2(225v^4 −480v^3 +166v^2 −32v+1))) squaring & transforming v^6 −2v^5 +((77v^4 )/(75))−((436v^3 )/(3375))−((49v^2 )/(5625))−((2v)/(50625))+(1/(50625))=0 No exact solution possible 0<v≤(1/(15)) ⇒ v≈.0385350883972 ⇒ u≈.681103226378 x≈.707349599414 y≈.654856853342](Q197905.png)
$$\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\geqslant\mathrm{0}\wedge\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }>\mathrm{0} \\ $$$$\mathrm{Let}\:{p}=\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\wedge{q}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\frac{{x}−{py}}{{q}}=\mathrm{2}\wedge\frac{{y}−{px}}{{q}}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\Leftrightarrow \\ $$$${x}=\frac{\left(\mathrm{7}{p}+\mathrm{8}\right){q}}{\mathrm{4}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)}\wedge{y}=\frac{\left(\mathrm{8}{p}+\mathrm{7}\right){q}}{\mathrm{4}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\:{x}−{y}=\frac{{q}}{\mathrm{4}\left(\mathrm{1}+{p}^{\mathrm{2}} \right)}>\mathrm{0}\:\Rightarrow\:{x}>{y}\:\left[\bigstar\right] \\ $$$$\frac{{x}−{y}\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\mathrm{2}\wedge\frac{{y}−{x}\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\Leftrightarrow \\ $$$$\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }=\frac{{x}−{y}\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{4}\left({y}−{x}\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\right)}{\mathrm{7}} \\ $$$$\Rightarrow \\ $$$$\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }=\frac{\mathrm{8}{y}−\mathrm{7}{x}}{\mathrm{8}{x}−\mathrm{7}{y}} \\ $$$$\left[\bigstar\right]\:\mathrm{Let}\:{x}={u}\left(\mathrm{1}+{v}\right)\wedge{y}={u}\left(\mathrm{1}−{v}\right)\wedge{u}>\mathrm{0}\wedge{v}>\mathrm{0} \\ $$$$\mathrm{2}\mid{u}\mid\sqrt{{v}}=\frac{\mathrm{1}−\mathrm{15}{v}}{\mathrm{1}+\mathrm{15}{v}}\:\Rightarrow\:\mathrm{0}<{v}\leqslant\frac{\mathrm{1}}{\mathrm{15}} \\ $$$${u}=\frac{\mathrm{1}−\mathrm{15}{v}}{\mathrm{2}\sqrt{{v}}\left(\mathrm{1}+\mathrm{15}{v}\right)} \\ $$$$\mathrm{Insert}\:\mathrm{in}\:\mathrm{the}\:\mathrm{following}\:\mathrm{equation}\:\&\:\mathrm{transform} \\ $$$${x}−{y}\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{16}{v}\left(\mathrm{1}−\mathrm{15}{v}\right)=\left(\mathrm{1}+\mathrm{15}{v}\right)\sqrt{−\mathrm{2}\left(\mathrm{225}{v}^{\mathrm{4}} −\mathrm{480}{v}^{\mathrm{3}} +\mathrm{166}{v}^{\mathrm{2}} −\mathrm{32}{v}+\mathrm{1}\right)} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming} \\ $$$${v}^{\mathrm{6}} −\mathrm{2}{v}^{\mathrm{5}} +\frac{\mathrm{77}{v}^{\mathrm{4}} }{\mathrm{75}}−\frac{\mathrm{436}{v}^{\mathrm{3}} }{\mathrm{3375}}−\frac{\mathrm{49}{v}^{\mathrm{2}} }{\mathrm{5625}}−\frac{\mathrm{2}{v}}{\mathrm{50625}}+\frac{\mathrm{1}}{\mathrm{50625}}=\mathrm{0} \\ $$$$\mathrm{No}\:\mathrm{exact}\:\mathrm{solution}\:\mathrm{possible} \\ $$$$\mathrm{0}<{v}\leqslant\frac{\mathrm{1}}{\mathrm{15}}\:\Rightarrow\:{v}\approx.\mathrm{0385350883972} \\ $$$$\Rightarrow\:{u}\approx.\mathrm{681103226378} \\ $$$${x}\approx.\mathrm{707349599414} \\ $$$${y}\approx.\mathrm{654856853342} \\ $$$$ \\ $$
Commented by cherokeesay last updated on 04/Oct/23

$${thank}\:{you}\:! \\ $$
Commented by Frix last updated on 04/Oct/23
��
