
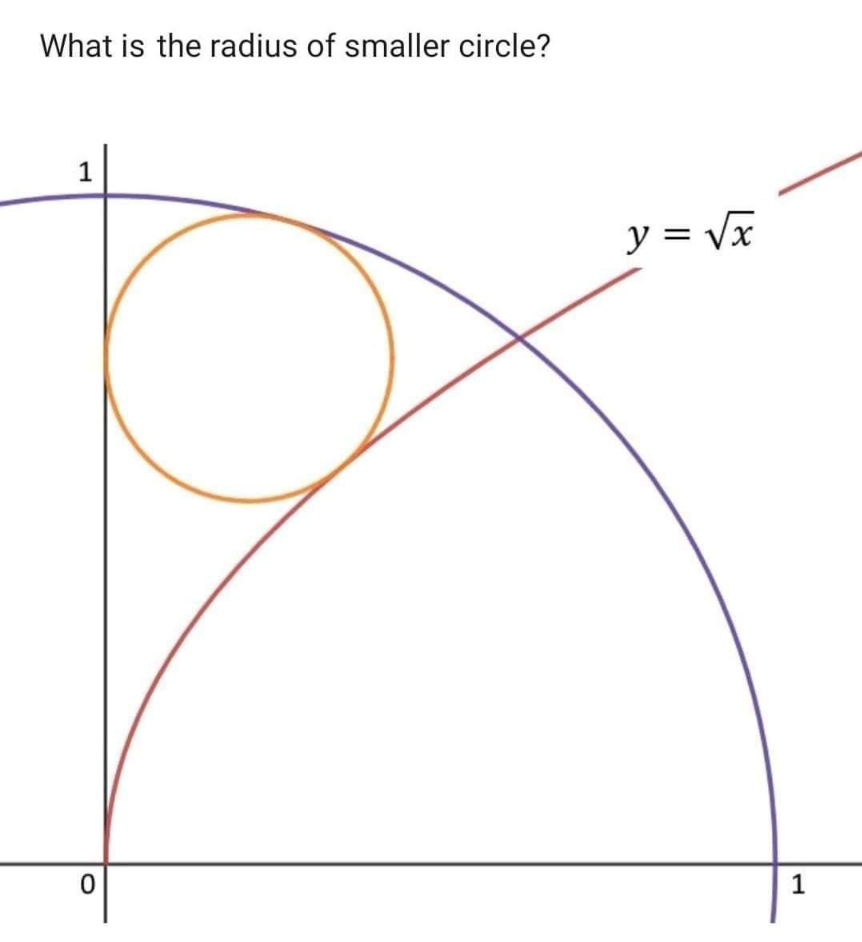
Question Number 197865 by Blackpanther last updated on 01/Oct/23
Answered by mr W last updated on 02/Oct/23
Commented by mr W last updated on 02/Oct/23
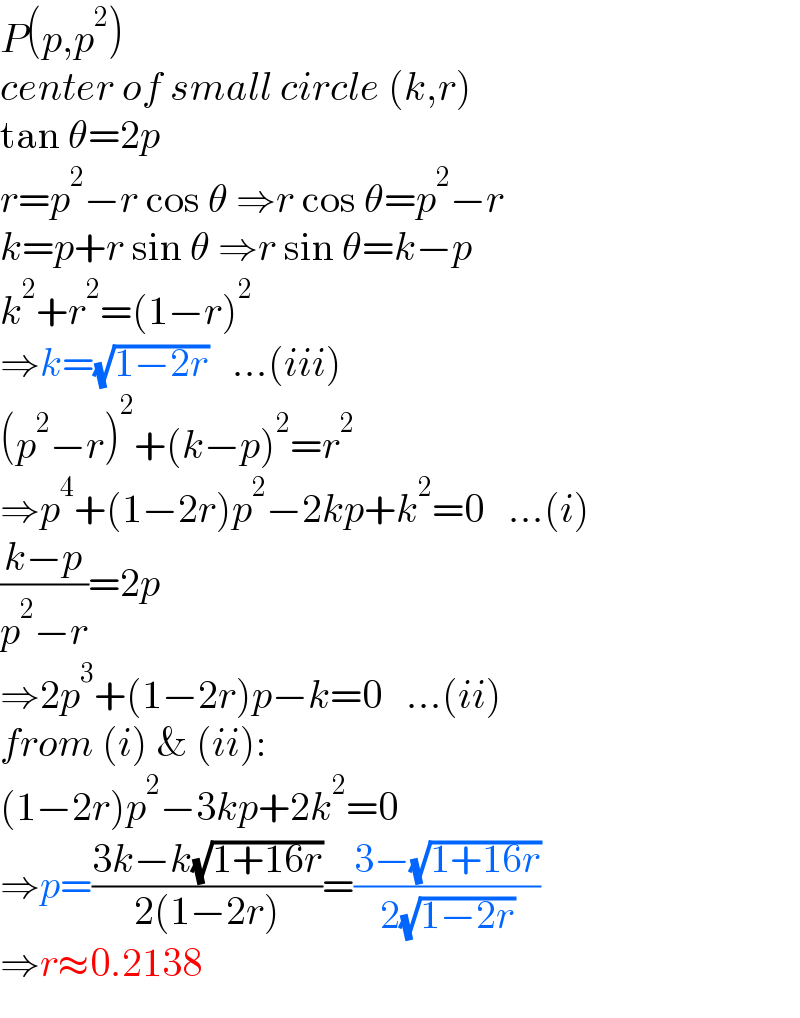
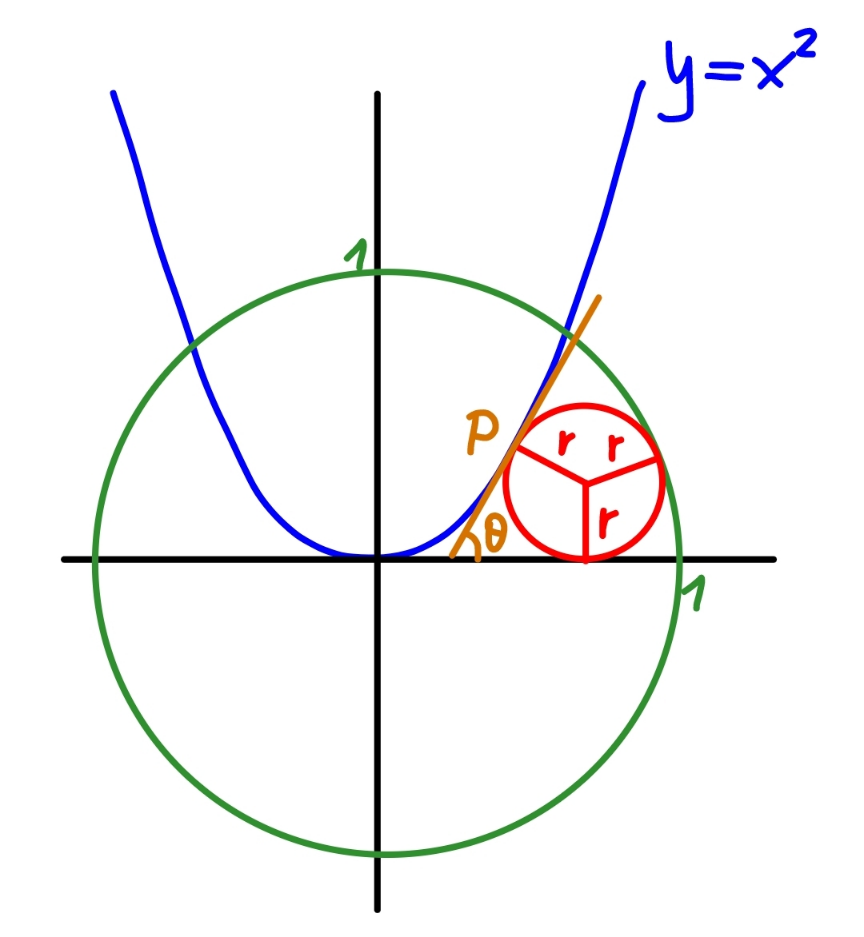
$${P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${center}\:{of}\:{small}\:{circle}\:\left({k},{r}\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$${r}={p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\theta\:\Rightarrow{r}\:\mathrm{cos}\:\theta={p}^{\mathrm{2}} −{r} \\ $$$${k}={p}+{r}\:\mathrm{sin}\:\theta\:\Rightarrow{r}\:\mathrm{sin}\:\theta={k}−{p} \\ $$$${k}^{\mathrm{2}} +{r}^{\mathrm{2}} =\left(\mathrm{1}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\sqrt{\mathrm{1}−\mathrm{2}{r}}\:\:\:...\left({iii}\right) \\ $$$$\left({p}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} +\left({k}−{p}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{p}^{\mathrm{4}} +\left(\mathrm{1}−\mathrm{2}{r}\right){p}^{\mathrm{2}} −\mathrm{2}{kp}+{k}^{\mathrm{2}} =\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\frac{{k}−{p}}{{p}^{\mathrm{2}} −{r}}=\mathrm{2}{p} \\ $$$$\Rightarrow\mathrm{2}{p}^{\mathrm{3}} +\left(\mathrm{1}−\mathrm{2}{r}\right){p}−{k}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:\&\:\left({ii}\right): \\ $$$$\left(\mathrm{1}−\mathrm{2}{r}\right){p}^{\mathrm{2}} −\mathrm{3}{kp}+\mathrm{2}{k}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{\mathrm{3}{k}−{k}\sqrt{\mathrm{1}+\mathrm{16}{r}}}{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{r}\right)}=\frac{\mathrm{3}−\sqrt{\mathrm{1}+\mathrm{16}{r}}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{2}{r}}} \\ $$$$\Rightarrow{r}\approx\mathrm{0}.\mathrm{2138} \\ $$
Commented by mr W last updated on 02/Oct/23

