Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 197838 by hardmath last updated on 30/Sep/23

Answered by MM42 last updated on 30/Sep/23

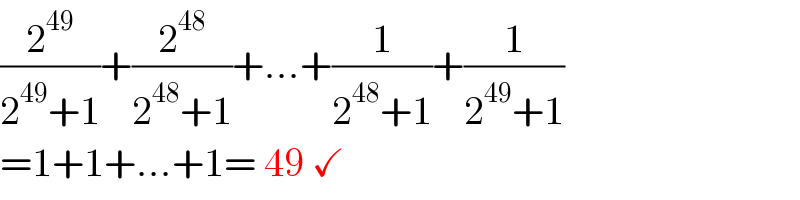
(2^(49) /(2^(49) +1))+(2^(48) /(2^(48) +1))+...+(1/(2^(48) +1))+(1/(2^(49) +1)) =1+1+...+1= 49 ✓

$$\frac{\mathrm{2}^{\mathrm{49}} }{\mathrm{2}^{\mathrm{49}} +\mathrm{1}}+\frac{\mathrm{2}^{\mathrm{48}} }{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}+...+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{49}} +\mathrm{1}} \\ $$$$=\mathrm{1}+\mathrm{1}+...+\mathrm{1}=\:\mathrm{49}\:\checkmark \\ $$

Commented by hardmath last updated on 30/Sep/23

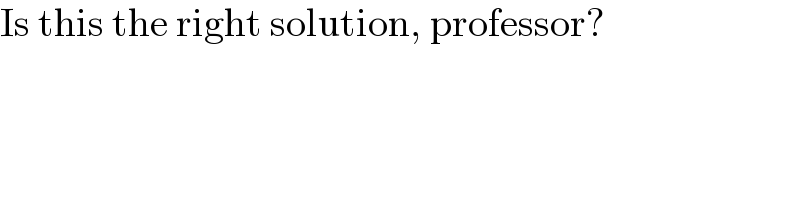
Is this the right solution, professor?

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{the}\:\mathrm{right}\:\mathrm{solution},\:\mathrm{professor}? \\ $$

Commented by cortano12 last updated on 01/Oct/23

49(1/2)

$$\mathrm{49}\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 01/Oct/23

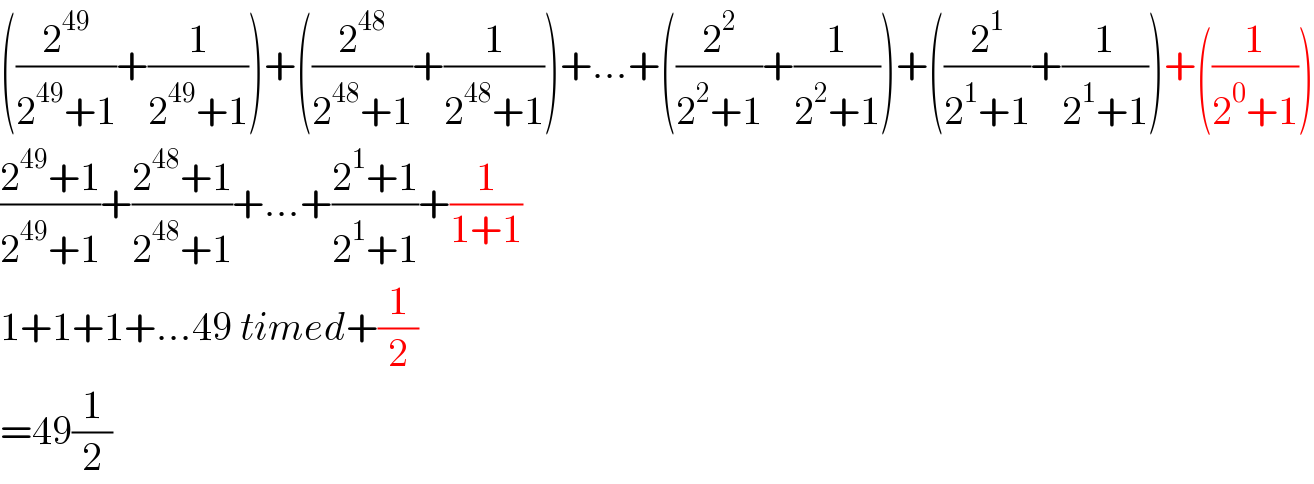
((2^(49) /(2^(49) +1))+(1/(2^(49) +1)))+((2^(48) /(2^(48) +1))+(1/(2^(48) +1)))+...+((2^2 /(2^2 +1))+(1/(2^2 +1)))+((2^1 /(2^1 +1))+(1/(2^1 +1)))+((1/(2^0 +1))) ((2^(49) +1)/(2^(49) +1))+((2^(48) +1)/(2^(48) +1))+...+((2^1 +1)/(2^1 +1))+(1/(1+1)) 1+1+1+...49 timed+(1/2) =49(1/2)

$$\left(\frac{\mathrm{2}^{\mathrm{49}} }{\mathrm{2}^{\mathrm{49}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{49}} +\mathrm{1}}\right)+\left(\frac{\mathrm{2}^{\mathrm{48}} }{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}\right)+...+\left(\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +\mathrm{1}}\right)+\left(\frac{\mathrm{2}^{\mathrm{1}} }{\mathrm{2}^{\mathrm{1}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} +\mathrm{1}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} +\mathrm{1}}\right) \\ $$$$\frac{\mathrm{2}^{\mathrm{49}} +\mathrm{1}}{\mathrm{2}^{\mathrm{49}} +\mathrm{1}}+\frac{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}+...+\frac{\mathrm{2}^{\mathrm{1}} +\mathrm{1}}{\mathrm{2}^{\mathrm{1}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}} \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{1}+...\mathrm{49}\:{timed}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{49}\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by MM42 last updated on 01/Oct/23

ok .✓

$${ok}\:.\checkmark \\ $$

Answered by Rasheed.Sindhi last updated on 02/Oct/23

AnOther way... (1/(2^(−49) +1))+(1/(2^(−48) +1))+...+(1/(2^(48) +1))+(1/(2^(49) +1)) =((1/(2^(−49) +1))+(1/(2^(49) +1)))+((1/(2^(−48) +1))+(1/(2^(48) +1)))+ ....+((1/(2^(−1) +1))+(1/(2^1 +1)))+((1/(2^0 +1))) =(((2^(49) +1+2^(−49) +1)/(1+2^(−49) +2^(49) +1)))+(((2^(48) +1+2^(−48) +1)/(1+2^(−48) +2^(48) +1)))+ ...+(((2^1 +1+2^(−1) +1)/(1+2^(−1) +2^1 +1)))+((1/(1+1))) =1+1+....+1(49 times)+(1/2) =49(1/2)

$$\mathrm{AnOther}\:\mathrm{way}... \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{−\mathrm{49}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{−\mathrm{48}} +\mathrm{1}}+...+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{49}} +\mathrm{1}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}^{−\mathrm{49}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{49}} +\mathrm{1}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{−\mathrm{48}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{48}} +\mathrm{1}}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....+\left(\frac{\mathrm{1}}{\mathrm{2}^{−\mathrm{1}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} +\mathrm{1}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} +\mathrm{1}}\right) \\ $$$$=\left(\frac{\mathrm{2}^{\mathrm{49}} +\mathrm{1}+\mathrm{2}^{−\mathrm{49}} +\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\mathrm{49}} +\mathrm{2}^{\mathrm{49}} +\mathrm{1}}\right)+\left(\frac{\mathrm{2}^{\mathrm{48}} +\mathrm{1}+\mathrm{2}^{−\mathrm{48}} +\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\mathrm{48}} +\mathrm{2}^{\mathrm{48}} +\mathrm{1}}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...+\left(\frac{\mathrm{2}^{\mathrm{1}} +\mathrm{1}+\mathrm{2}^{−\mathrm{1}} +\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\mathrm{1}} +\mathrm{2}^{\mathrm{1}} +\mathrm{1}}\right)+\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}\right) \\ $$$$=\mathrm{1}+\mathrm{1}+....+\mathrm{1}\left(\mathrm{49}\:{times}\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{49}\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com