Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 197776 by universe last updated on 28/Sep/23

Commented by witcher3 last updated on 28/Sep/23

∣n_(−−) what is ?

$$\mid\underset{−−} {\mathrm{n}}\:\:\:\mathrm{what}\:\mathrm{is}\:? \\ $$

Commented by universe last updated on 28/Sep/23

this is a symbol of factorial

$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{symbol}\:\mathrm{of}\:\mathrm{factorial} \\ $$$$ \\ $$

Commented by mr W last updated on 28/Sep/23

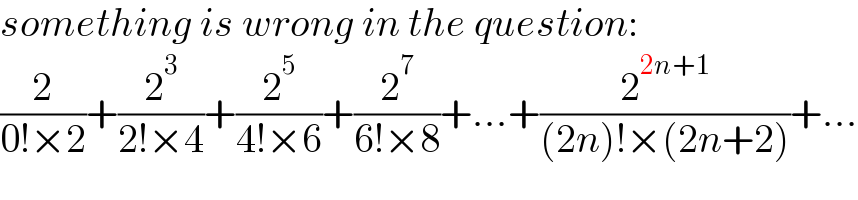
something is wrong in the question: (2/(0!×2))+(2^3 /(2!×4))+(2^5 /(4!×6))+(2^7 /(6!×8))+...+(2^(2n+1) /((2n)!×(2n+2)))+...

$${something}\:{is}\:{wrong}\:{in}\:{the}\:{question}: \\ $$$$\frac{\mathrm{2}}{\mathrm{0}!×\mathrm{2}}+\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{2}!×\mathrm{4}}+\frac{\mathrm{2}^{\mathrm{5}} }{\mathrm{4}!×\mathrm{6}}+\frac{\mathrm{2}^{\mathrm{7}} }{\mathrm{6}!×\mathrm{8}}+...+\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}\right)!×\left(\mathrm{2}{n}+\mathrm{2}\right)}+... \\ $$

Answered by mr W last updated on 28/Sep/23

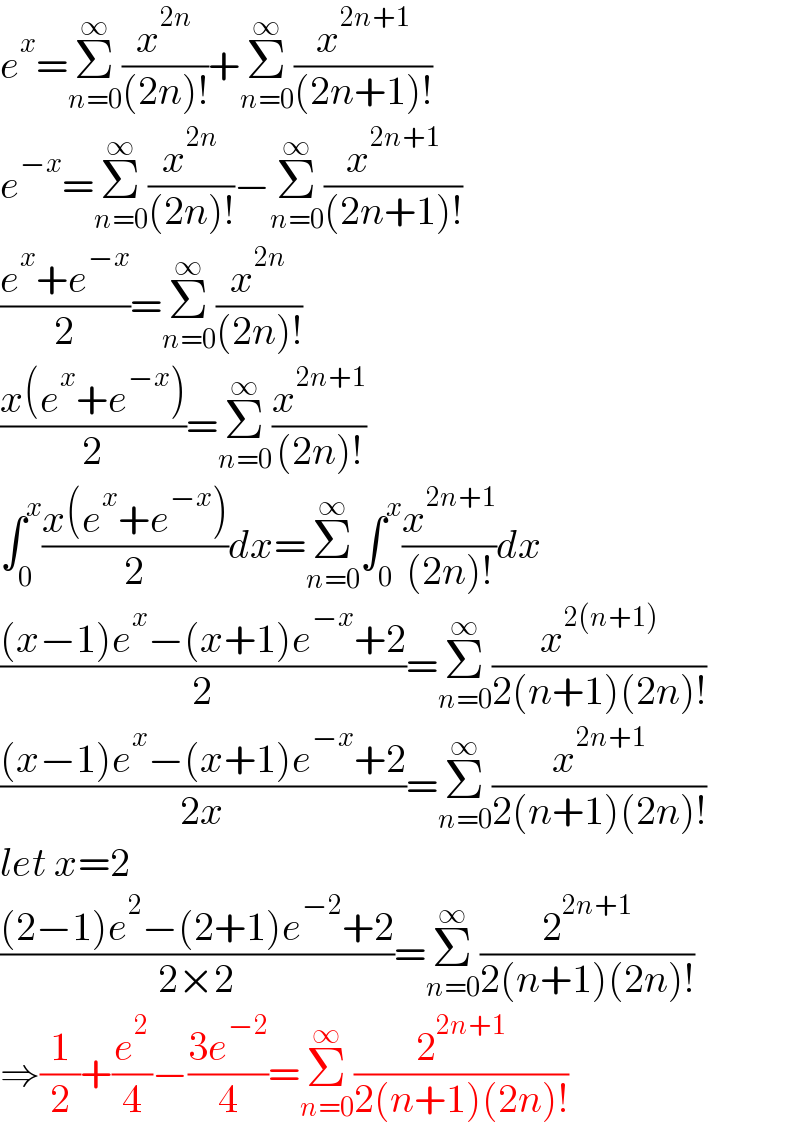
e^x =Σ_(n=0) ^∞ (x^(2n) /((2n)!))+Σ_(n=0) ^∞ (x^(2n+1) /((2n+1)!)) e^(−x) =Σ_(n=0) ^∞ (x^(2n) /((2n)!))−Σ_(n=0) ^∞ (x^(2n+1) /((2n+1)!)) ((e^x +e^(−x) )/2)=Σ_(n=0) ^∞ (x^(2n) /((2n)!)) ((x(e^x +e^(−x) ))/2)=Σ_(n=0) ^∞ (x^(2n+1) /((2n)!)) ∫_0 ^x ((x(e^x +e^(−x) ))/2)dx=Σ_(n=0) ^∞ ∫_0 ^x (x^(2n+1) /((2n)!))dx (((x−1)e^x −(x+1)e^(−x) +2)/2)=Σ_(n=0) ^∞ (x^(2(n+1)) /(2(n+1)(2n)!)) (((x−1)e^x −(x+1)e^(−x) +2)/(2x))=Σ_(n=0) ^∞ (x^(2n+1) /(2(n+1)(2n)!)) let x=2 (((2−1)e^2 −(2+1)e^(−2) +2)/(2×2))=Σ_(n=0) ^∞ (2^(2n+1) /(2(n+1)(2n)!)) ⇒(1/2)+(e^2 /4)−((3e^(−2) )/4)=Σ_(n=0) ^∞ (2^(2n+1) /(2(n+1)(2n)!))

$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${e}^{−{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$\frac{{x}\left({e}^{{x}} +{e}^{−{x}} \right)}{\mathrm{2}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$\int_{\mathrm{0}} ^{{x}} \frac{{x}\left({e}^{{x}} +{e}^{−{x}} \right)}{\mathrm{2}}{dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} \frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}\right)!}{dx} \\ $$$$\frac{\left({x}−\mathrm{1}\right){e}^{{x}} −\left({x}+\mathrm{1}\right){e}^{−{x}} +\mathrm{2}}{\mathrm{2}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}\left({n}+\mathrm{1}\right)} }{\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!} \\ $$$$\frac{\left({x}−\mathrm{1}\right){e}^{{x}} −\left({x}+\mathrm{1}\right){e}^{−{x}} +\mathrm{2}}{\mathrm{2}{x}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!} \\ $$$${let}\:{x}=\mathrm{2} \\ $$$$\frac{\left(\mathrm{2}−\mathrm{1}\right){e}^{\mathrm{2}} −\left(\mathrm{2}+\mathrm{1}\right){e}^{−\mathrm{2}} +\mathrm{2}}{\mathrm{2}×\mathrm{2}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}+\frac{{e}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{3}{e}^{−\mathrm{2}} }{\mathrm{4}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!} \\ $$

Commented by universe last updated on 28/Sep/23

thanks sir

$${thanks}\:{sir}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com