
Question Number 197740 by cortano12 last updated on 27/Sep/23
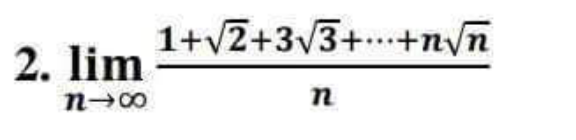
Answered by mr W last updated on 27/Sep/23
![lim_(n→∞) Σ_(k=1) ^n ((k(√k))/n) =lim_(n→∞) ((n(√n))/n)Σ_(k=1) ^n ((k(√k))/(n(√n))) =(lim_(n→∞) n(√n))[lim_(n→∞) (1/n)Σ_(k=1) ^n ((k/n)(√(k/n)))] =(lim_(n→∞) n(√n))[∫_0 ^1 x(√x)dx] =(lim_(n→∞) n(√n))×(2/5) =∞](Q197745.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}\sqrt{{k}}}{{n}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}\sqrt{{n}}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}\sqrt{{k}}}{{n}\sqrt{{n}}} \\ $$$$=\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}\sqrt{{n}}\right)\left[\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{k}}{{n}}\sqrt{\frac{{k}}{{n}}}\right)\right] \\ $$$$=\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}\sqrt{{n}}\right)\left[\int_{\mathrm{0}} ^{\mathrm{1}} {x}\sqrt{{x}}{dx}\right] \\ $$$$=\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}\sqrt{{n}}\right)×\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$=\infty \\ $$
Answered by witcher3 last updated on 27/Sep/23

$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\sqrt{\mathrm{k}}\geqslant\mathrm{n}\sqrt{\mathrm{n}} \\ $$$$\frac{\Sigma\mathrm{k}\sqrt{\mathrm{k}}}{\mathrm{n}}\geqslant\sqrt{\mathrm{n}}\rightarrow\infty \\ $$
Answered by Frix last updated on 27/Sep/23
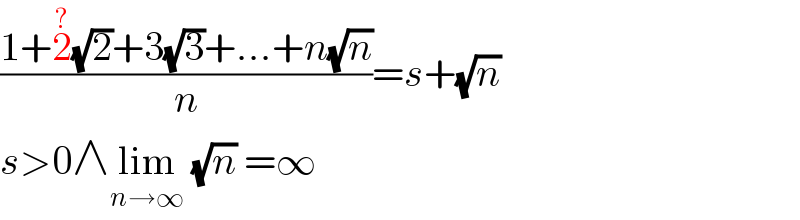
$$\frac{\mathrm{1}+\overset{?} {\mathrm{2}}\sqrt{\mathrm{2}}+\mathrm{3}\sqrt{\mathrm{3}}+...+{n}\sqrt{{n}}}{{n}}={s}+\sqrt{{n}} \\ $$$${s}>\mathrm{0}\wedge\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{n}}\:=\infty \\ $$
