Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 197730 by ajfour last updated on 27/Sep/23

Commented by ajfour last updated on 27/Sep/23

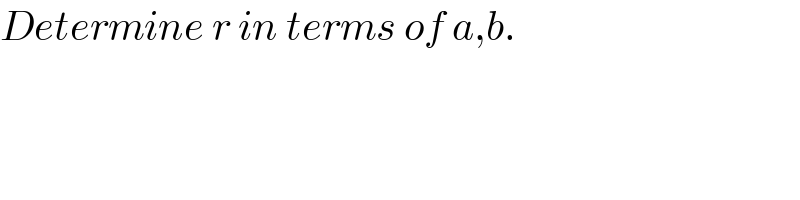
Determine r in terms of a,b.

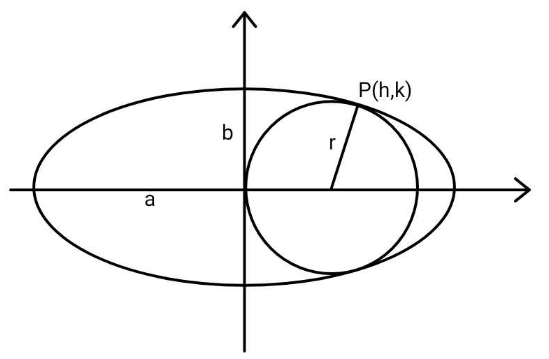
$${Determine}\:{r}\:{in}\:{terms}\:{of}\:{a},{b}. \\ $$

Commented by ajfour last updated on 27/Sep/23

https://youtu.be/0sSIzDZtOBQ?si=jQAFPvy744djWIga

Commented by ajfour last updated on 27/Sep/23

My lecture on You tube Differentiation : Lesson 2

$${My}\:{lecture}\:{on}\:{You}\:{tube}\: \\ $$$${Differentiation}\::\:{Lesson}\:\mathrm{2} \\ $$

Answered by mr W last updated on 27/Sep/23

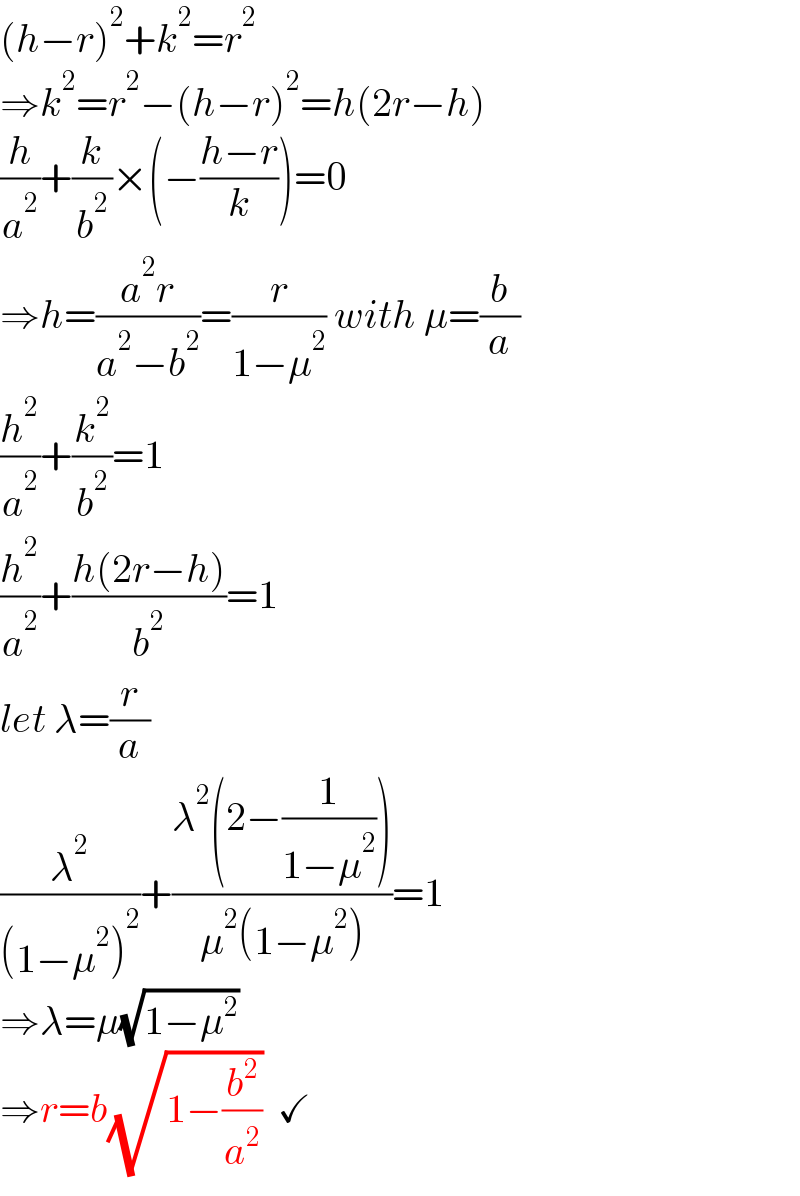
(h−r)^2 +k^2 =r^2 ⇒k^2 =r^2 −(h−r)^2 =h(2r−h) (h/a^2 )+(k/b^2 )×(−((h−r)/k))=0 ⇒h=((a^2 r)/(a^2 −b^2 ))=(r/(1−μ^2 )) with μ=(b/a) (h^2 /a^2 )+(k^2 /b^2 )=1 (h^2 /a^2 )+((h(2r−h))/b^2 )=1 let λ=(r/a) (λ^2 /((1−μ^2 )^2 ))+((λ^2 (2−(1/(1−μ^2 ))))/(μ^2 (1−μ^2 )))=1 ⇒λ=μ(√(1−μ^2 )) ⇒r=b(√(1−(b^2 /a^2 ))) ✓

$$\left({h}−{r}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{k}^{\mathrm{2}} ={r}^{\mathrm{2}} −\left({h}−{r}\right)^{\mathrm{2}} ={h}\left(\mathrm{2}{r}−{h}\right) \\ $$$$\frac{{h}}{{a}^{\mathrm{2}} }+\frac{{k}}{{b}^{\mathrm{2}} }×\left(−\frac{{h}−{r}}{{k}}\right)=\mathrm{0} \\ $$$$\Rightarrow{h}=\frac{{a}^{\mathrm{2}} {r}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\frac{{r}}{\mathrm{1}−\mu^{\mathrm{2}} }\:{with}\:\mu=\frac{{b}}{{a}} \\ $$$$\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{h}\left(\mathrm{2}{r}−{h}\right)}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${let}\:\lambda=\frac{{r}}{{a}} \\ $$$$\frac{\lambda^{\mathrm{2}} }{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\lambda^{\mathrm{2}} \left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{1}−\mu^{\mathrm{2}} }\right)}{\mu^{\mathrm{2}} \left(\mathrm{1}−\mu^{\mathrm{2}} \right)}=\mathrm{1} \\ $$$$\Rightarrow\lambda=\mu\sqrt{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\Rightarrow{r}={b}\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:\:\checkmark \\ $$

Commented by mr W last updated on 27/Sep/23

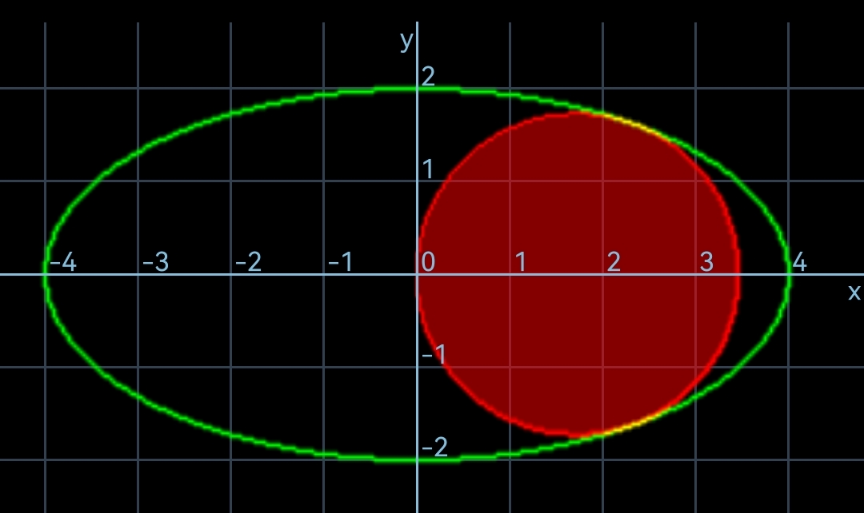
Commented by ajfour last updated on 27/Sep/23

Yes sir. Thank you.

Answered by ajfour last updated on 27/Sep/23

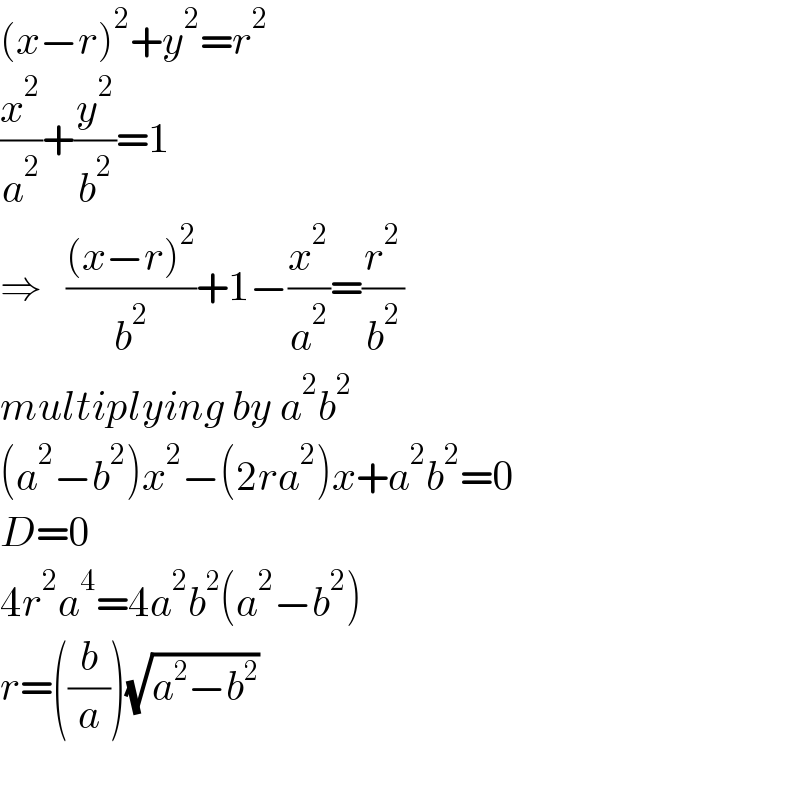
(x−r)^2 +y^2 =r^2 (x^2 /a^2 )+(y^2 /b^2 )=1 ⇒ (((x−r)^2 )/b^2 )+1−(x^2 /a^2 )=(r^2 /b^2 ) multiplying by a^2 b^2 (a^2 −b^2 )x^2 −(2ra^2 )x+a^2 b^2 =0 D=0 4r^2 a^4 =4a^2 b^2 (a^2 −b^2 ) r=((b/a))(√(a^2 −b^2 ))

$$\left({x}−{r}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\frac{\left({x}−{r}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${multiplying}\:{by}\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} −\left(\mathrm{2}{ra}^{\mathrm{2}} \right){x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${D}=\mathrm{0} \\ $$$$\mathrm{4}{r}^{\mathrm{2}} {a}^{\mathrm{4}} =\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$${r}=\left(\frac{{b}}{{a}}\right)\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$ \\ $$

Commented by mr W last updated on 27/Sep/23

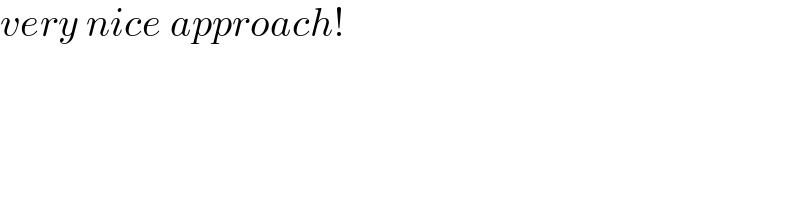
very nice approach!

$${very}\:{nice}\:{approach}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com