Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 197365 by mokys last updated on 15/Sep/23

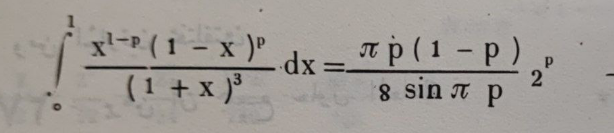
Answered by witcher3 last updated on 15/Sep/23

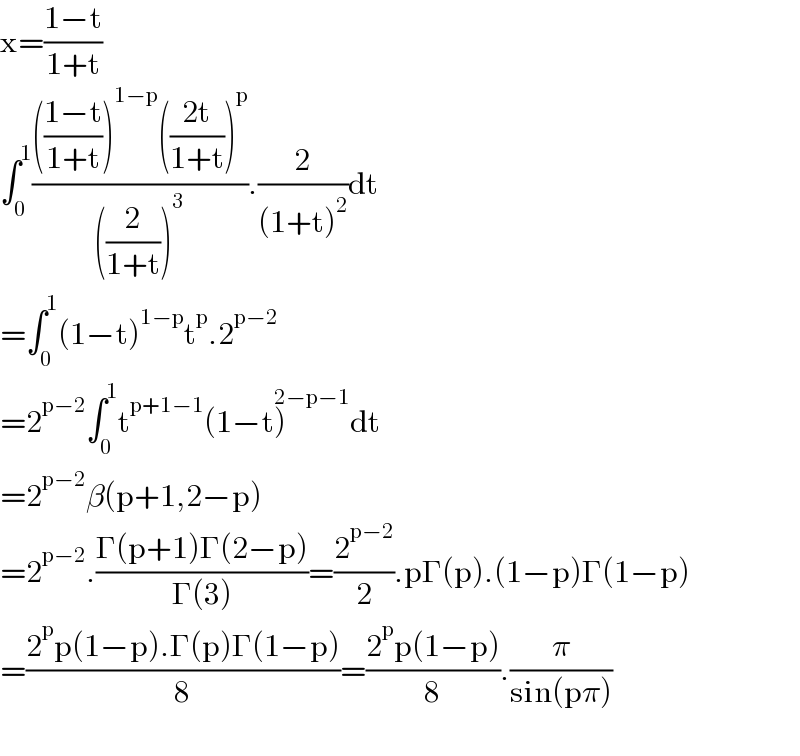
x=((1−t)/(1+t)) ∫_0 ^1 (((((1−t)/(1+t)))^(1−p) (((2t)/(1+t)))^p )/(((2/(1+t)))^3 )).(2/((1+t)^2 ))dt =∫_0 ^1 (1−t)^(1−p) t^p .2^(p−2) =2^(p−2) ∫_0 ^1 t^(p+1−1) (1−t)^(2−p−1) dt =2^(p−2) β(p+1,2−p) =2^(p−2) .((Γ(p+1)Γ(2−p))/(Γ(3)))=(2^(p−2) /2).pΓ(p).(1−p)Γ(1−p) =((2^p p(1−p).Γ(p)Γ(1−p))/8)=((2^p p(1−p))/8).(π/(sin(pπ)))

$$\mathrm{x}=\frac{\mathrm{1}−\mathrm{t}}{\mathrm{1}+\mathrm{t}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\frac{\mathrm{1}−\mathrm{t}}{\mathrm{1}+\mathrm{t}}\right)^{\mathrm{1}−\mathrm{p}} \left(\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}}\right)^{\mathrm{p}} }{\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}}\right)^{\mathrm{3}} }.\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{1}−\mathrm{p}} \mathrm{t}^{\mathrm{p}} .\mathrm{2}^{\mathrm{p}−\mathrm{2}} \\ $$$$=\mathrm{2}^{\mathrm{p}−\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}^{\mathrm{p}+\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\overset{\mathrm{2}−\mathrm{p}−\mathrm{1}} {\right)}\mathrm{dt} \\ $$$$=\mathrm{2}^{\mathrm{p}−\mathrm{2}} \beta\left(\mathrm{p}+\mathrm{1},\mathrm{2}−\mathrm{p}\right) \\ $$$$=\mathrm{2}^{\mathrm{p}−\mathrm{2}} .\frac{\Gamma\left(\mathrm{p}+\mathrm{1}\right)\Gamma\left(\mathrm{2}−\mathrm{p}\right)}{\Gamma\left(\mathrm{3}\right)}=\frac{\mathrm{2}^{\mathrm{p}−\mathrm{2}} }{\mathrm{2}}.\mathrm{p}\Gamma\left(\mathrm{p}\right).\left(\mathrm{1}−\mathrm{p}\right)\Gamma\left(\mathrm{1}−\mathrm{p}\right) \\ $$$$=\frac{\mathrm{2}^{\mathrm{p}} \mathrm{p}\left(\mathrm{1}−\mathrm{p}\right).\Gamma\left(\mathrm{p}\right)\Gamma\left(\mathrm{1}−\mathrm{p}\right)}{\mathrm{8}}=\frac{\mathrm{2}^{\mathrm{p}} \mathrm{p}\left(\mathrm{1}−\mathrm{p}\right)}{\mathrm{8}}.\frac{\pi}{\mathrm{sin}\left(\mathrm{p}\pi\right)} \\ $$$$ \\ $$

Commented by mokys last updated on 15/Sep/23

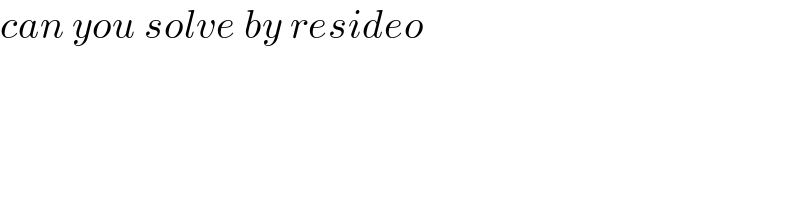
can you solve by resideo

$${can}\:{you}\:{solve}\:{by}\:{resideo} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com