
Question Number 197346 by Amidip last updated on 14/Sep/23
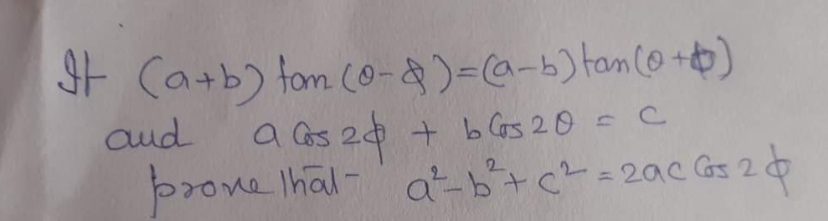
Answered by som(math1967) last updated on 14/Sep/23
![((a+b)/(a−b))=((tan(θ+φ))/(tan(θ−φ))) ((a+b)/(a−b))=((sin(θ+φ)cos(θ−φ))/(sin(θ−φ)cos(θ+φ))) ((2a)/(2b))=((sin2θ)/(sin2φ)) [using componendo÷ndo] asin2φ=bsin2θ a^2 sin^2 2φ=b^2 sin^2 2θ a^2 −b^2 =a^2 cos^2 2φ−b^2 cos^2 2θ now given acos2φ+bcos2θ=c (acos2φ−c)^2 =b^2 cos^2 2θ a^2 cos^2 2φ−2accos 2φ+c^2 =b^2 cos^2 2θ a^2 cos^2 2φ−b^2 cos^2 2θ +c^2 =2accos2φ a^2 −b^2 +c^2 =2accos2φ [∵a^2 cos^2 2φ−b^2 cos^2 2θ =a^2 −b^2 ]](Q197347.png)
$$\:\frac{{a}+{b}}{{a}−{b}}=\frac{{tan}\left(\theta+\phi\right)}{{tan}\left(\theta−\phi\right)} \\ $$$$\:\frac{{a}+{b}}{{a}−{b}}=\frac{{sin}\left(\theta+\phi\right){cos}\left(\theta−\phi\right)}{{sin}\left(\theta−\phi\right){cos}\left(\theta+\phi\right)} \\ $$$$\frac{\mathrm{2}{a}}{\mathrm{2}{b}}=\frac{{sin}\mathrm{2}\theta}{{sin}\mathrm{2}\phi}\:\:\left[{using}\:{componendo\÷ndo}\right] \\ $$$${asin}\mathrm{2}\phi={bsin}\mathrm{2}\theta \\ $$$${a}^{\mathrm{2}} {sin}^{\mathrm{2}} \mathrm{2}\phi={b}^{\mathrm{2}} {sin}^{\mathrm{2}} \mathrm{2}\theta \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={a}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\phi−{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\theta\:\: \\ $$$${now}\:{given} \\ $$$${acos}\mathrm{2}\phi+{bcos}\mathrm{2}\theta={c} \\ $$$$\left({acos}\mathrm{2}\phi−{c}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\theta \\ $$$${a}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\phi−\mathrm{2}{ac}\mathrm{cos}\:\mathrm{2}\phi+{c}^{\mathrm{2}} ={b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta \\ $$$${a}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\phi−{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\theta\:\:+{c}^{\mathrm{2}} =\mathrm{2}{accos}\mathrm{2}\phi \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2}{accos}\mathrm{2}\phi \\ $$$$\left[\because{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\phi−{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \mathrm{2}\theta\:\:={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right] \\ $$
