
Question Number 197081 by sonukgindia last updated on 07/Sep/23
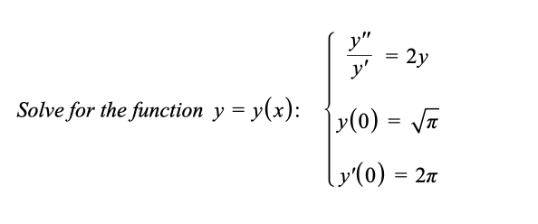
Commented by sonukgindia last updated on 07/Sep/23

$${check}\:{once} \\ $$
Commented by mokys last updated on 07/Sep/23
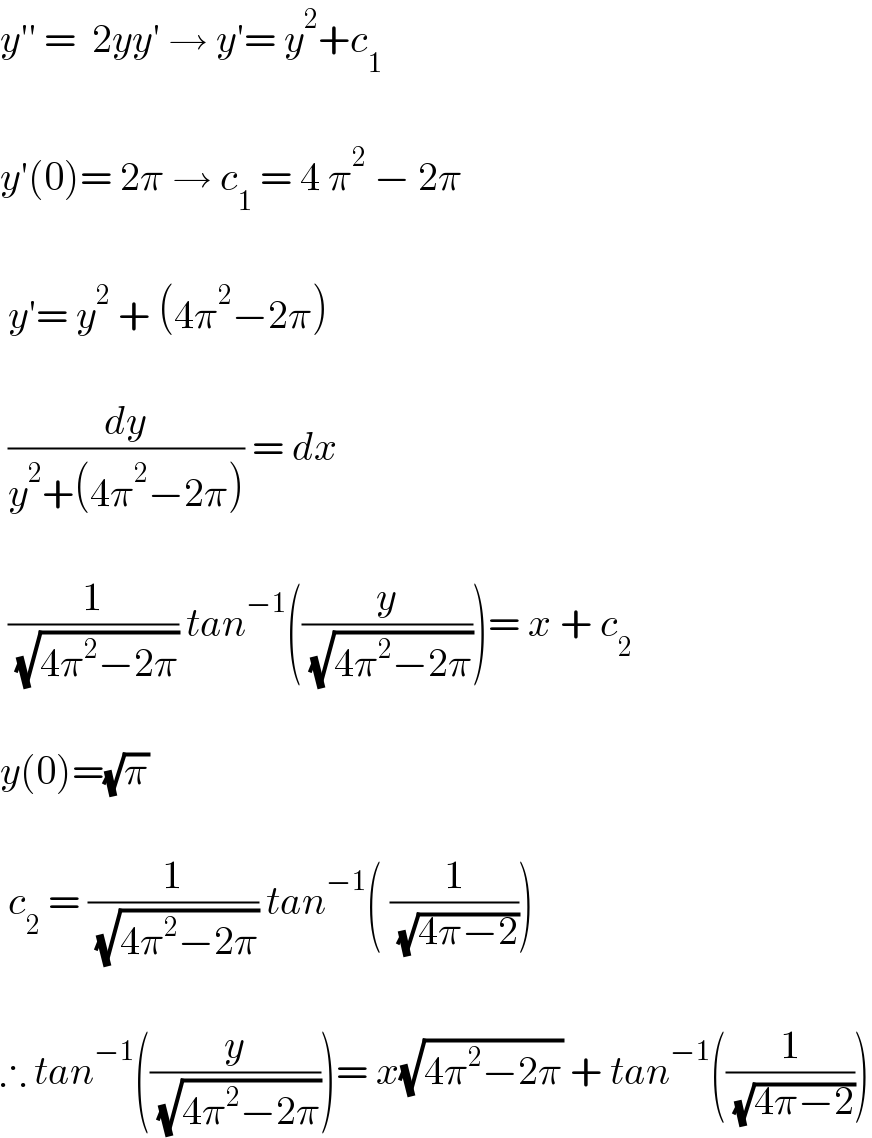
$${y}''\:=\:\:\mathrm{2}{yy}'\:\rightarrow\:{y}'=\:{y}^{\mathrm{2}} +{c}_{\mathrm{1}} \\ $$$$ \\ $$$${y}'\left(\mathrm{0}\right)=\:\mathrm{2}\pi\:\rightarrow\:{c}_{\mathrm{1}} \:=\:\mathrm{4}\:\pi^{\mathrm{2}} \:−\:\mathrm{2}\pi \\ $$$$ \\ $$$$\:{y}'=\:{y}^{\mathrm{2}} \:+\:\left(\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi\right) \\ $$$$ \\ $$$$\:\frac{{dy}}{{y}^{\mathrm{2}} +\left(\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi\right)}\:=\:{dx} \\ $$$$ \\ $$$$\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi}}\:{tan}^{−\mathrm{1}} \left(\frac{{y}}{\:\sqrt{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi}}\right)=\:{x}\:+\:{c}_{\mathrm{2}} \: \\ $$$$ \\ $$$${y}\left(\mathrm{0}\right)=\sqrt{\pi} \\ $$$$ \\ $$$$\:{c}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi}}\:{tan}^{−\mathrm{1}} \left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}\pi−\mathrm{2}}}\right) \\ $$$$ \\ $$$$\therefore\:{tan}^{−\mathrm{1}} \left(\frac{{y}}{\:\sqrt{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi}}\right)=\:{x}\sqrt{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{2}\pi}\:+\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}\pi−\mathrm{2}}}\right) \\ $$
Commented by sonukgindia last updated on 07/Sep/23
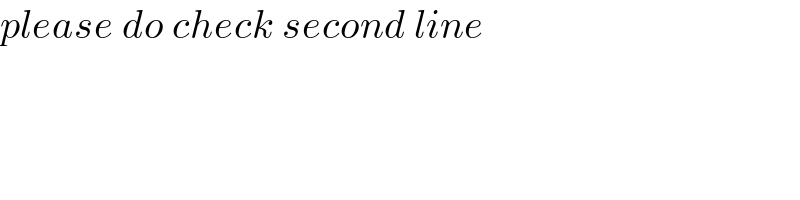
$${please}\:{do}\:{check}\:{second}\:{line}\: \\ $$
Commented by mokys last updated on 07/Sep/23

$${no}\:{problems} \\ $$
Commented by MathematicalUser2357 last updated on 10/Sep/23

$${check}\:{twoce} \\ $$
