Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 197073 by Abdullahrussell last updated on 07/Sep/23

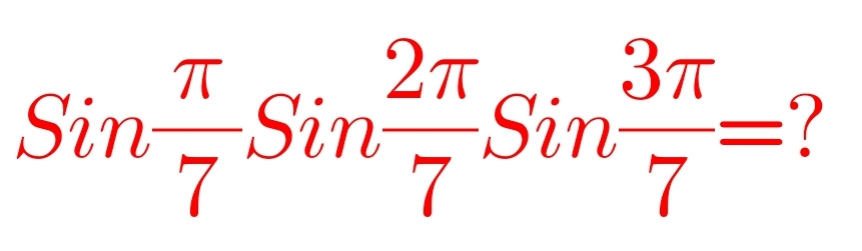
Answered by Frix last updated on 07/Sep/23

sin (π/7) sin ((2π)/7) sin ((3π)/7) =x Use trigonometric formulas to get (1/4)(cos ((3π)/(14)) +cos (π/(14)) −sin (π/7))=x (1) Now comes the “trick” (cos ((3π)/(14)) +cos (π/(14)) −sin (π/7))^3 =64x^3 Again use trigonometric formulas to get (7/4)(cos ((3π)/(14)) +cos (π/(14)) −sin (π/7))=64x^3 (2) ⇒ 4x=((256x^3 )/7) we know x>0 ⇒ x=((√7)/8)

$$\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{7}}\:={x} \\ $$$$\mathrm{Use}\:\mathrm{trigonometric}\:\mathrm{formulas}\:\mathrm{to}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{14}}\:+\mathrm{cos}\:\frac{\pi}{\mathrm{14}}\:−\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right)={x}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Now}\:\mathrm{comes}\:\mathrm{the}\:``\mathrm{trick}'' \\ $$$$\left(\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{14}}\:+\mathrm{cos}\:\frac{\pi}{\mathrm{14}}\:−\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right)^{\mathrm{3}} =\mathrm{64}{x}^{\mathrm{3}} \\ $$$$\mathrm{Again}\:\mathrm{use}\:\mathrm{trigonometric}\:\mathrm{formulas}\:\mathrm{to}\:\mathrm{get} \\ $$$$\frac{\mathrm{7}}{\mathrm{4}}\left(\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{14}}\:+\mathrm{cos}\:\frac{\pi}{\mathrm{14}}\:−\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right)=\mathrm{64}{x}^{\mathrm{3}} \:\left(\mathrm{2}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{x}=\frac{\mathrm{256}{x}^{\mathrm{3}} }{\mathrm{7}} \\ $$$$\mathrm{we}\:\mathrm{know}\:{x}>\mathrm{0}\:\Rightarrow\:{x}=\frac{\sqrt{\mathrm{7}}}{\mathrm{8}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com