Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 196946 by Khalmohmmad last updated on 04/Sep/23

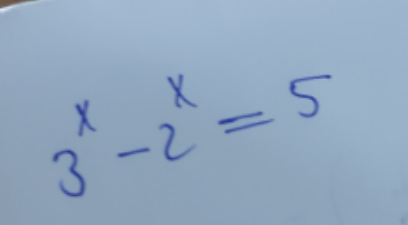
Answered by trisetyo last updated on 04/Sep/23

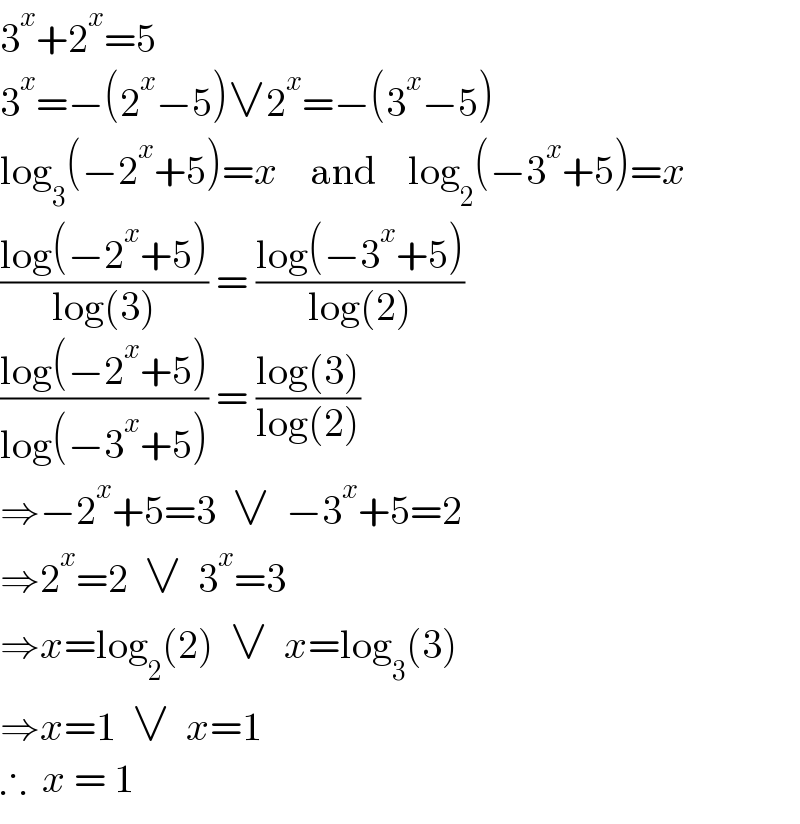
3^x +2^x =5 3^x =−(2^x −5)∨2^x =−(3^x −5) log_3 (−2^x +5)=x and log_2 (−3^x +5)=x ((log(−2^x +5))/(log(3))) = ((log(−3^x +5))/(log(2))) ((log(−2^x +5))/(log(−3^x +5))) = ((log(3))/(log(2))) ⇒−2^x +5=3 ∨ −3^x +5=2 ⇒2^x =2 ∨ 3^x =3 ⇒x=log_2 (2) ∨ x=log_3 (3) ⇒x=1 ∨ x=1 ∴ x = 1

$$\mathrm{3}^{{x}} +\mathrm{2}^{{x}} =\mathrm{5} \\ $$$$\mathrm{3}^{{x}} =−\left(\mathrm{2}^{{x}} −\mathrm{5}\right)\vee\mathrm{2}^{{x}} =−\left(\mathrm{3}^{{x}} −\mathrm{5}\right) \\ $$$$\mathrm{log}_{\mathrm{3}} \left(−\mathrm{2}^{{x}} +\mathrm{5}\right)={x}\:\:\:\:\mathrm{and}\:\:\:\:\mathrm{log}_{\mathrm{2}} \left(−\mathrm{3}^{{x}} +\mathrm{5}\right)={x} \\ $$$$\frac{\mathrm{log}\left(−\mathrm{2}^{{x}} +\mathrm{5}\right)}{\mathrm{log}\left(\mathrm{3}\right)}\:=\:\frac{\mathrm{log}\left(−\mathrm{3}^{{x}} +\mathrm{5}\right)}{\mathrm{log}\left(\mathrm{2}\right)} \\ $$$$\frac{\mathrm{log}\left(−\mathrm{2}^{{x}} +\mathrm{5}\right)}{\mathrm{log}\left(−\mathrm{3}^{{x}} +\mathrm{5}\right)}\:=\:\frac{\mathrm{log}\left(\mathrm{3}\right)}{\mathrm{log}\left(\mathrm{2}\right)} \\ $$$$\Rightarrow−\mathrm{2}^{{x}} +\mathrm{5}=\mathrm{3}\:\:\vee\:\:−\mathrm{3}^{{x}} +\mathrm{5}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}^{{x}} =\mathrm{2}\:\:\vee\:\:\mathrm{3}^{{x}} =\mathrm{3} \\ $$$$\Rightarrow{x}=\mathrm{log}_{\mathrm{2}} \left(\mathrm{2}\right)\:\:\vee\:\:{x}=\mathrm{log}_{\mathrm{3}} \left(\mathrm{3}\right) \\ $$$$\Rightarrow{x}=\mathrm{1}\:\:\vee\:\:{x}=\mathrm{1} \\ $$$$\therefore\:\:{x}\:=\:\mathrm{1} \\ $$

Commented by Frix last updated on 04/Sep/23

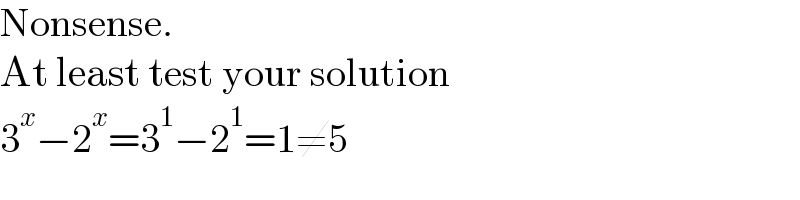
Nonsense. At least test your solution 3^x −2^x =3^1 −2^1 =1≠5

$$\mathrm{Nonsense}. \\ $$$$\mathrm{At}\:\mathrm{least}\:\mathrm{test}\:\mathrm{your}\:\mathrm{solution} \\ $$$$\mathrm{3}^{{x}} −\mathrm{2}^{{x}} =\mathrm{3}^{\mathrm{1}} −\mathrm{2}^{\mathrm{1}} =\mathrm{1}\neq\mathrm{5} \\ $$

Commented by trisetyo last updated on 04/Sep/23

oh i′m sorry... its 3^x −2^x =5 my answer 3^x +2^x =5 it was my mistake, sorry..

$$ \\ $$$$\mathrm{oh}\:\mathrm{i}'\mathrm{m}\:\mathrm{sorry}...\:\mathrm{its}\:\mathrm{3}^{{x}} −\mathrm{2}^{{x}} =\mathrm{5} \\ $$$$\mathrm{my}\:\mathrm{answer}\:\mathrm{3}^{{x}} +\mathrm{2}^{{x}} =\mathrm{5} \\ $$$$\mathrm{it}\:\mathrm{was}\:\mathrm{my}\:\mathrm{mistake},\:{sorry}.. \\ $$

Answered by Frix last updated on 04/Sep/23

3^2 −2^2 =9−4=5 x=2

$$\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} =\mathrm{9}−\mathrm{4}=\mathrm{5} \\ $$$${x}=\mathrm{2} \\ $$

Commented by trisetyo last updated on 04/Sep/23

verry simple solution XD

$$ \\ $$$${verry}\:{simple}\:{solution}\:{XD} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com