
Question Number 196914 by SANOGO last updated on 03/Sep/23
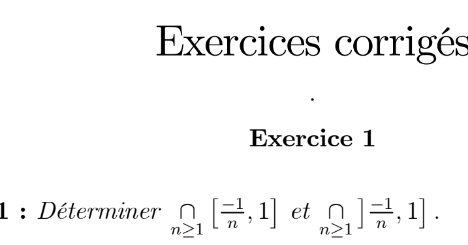
Answered by witcher3 last updated on 03/Sep/23
![−(1/(n+1))>−(1/n) I_n =[−(1/n),1] I_(n+1) ⊆I_n suite decroissante minore cv vers lim inf I_n =lim_(n→∞) I_n =[0,1] ∪_(n≥) I_n =I_1 =]−1,1]](Q196932.png)
$$−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}>−\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\mathrm{I}_{\mathrm{n}} =\left[−\frac{\mathrm{1}}{\mathrm{n}},\mathrm{1}\right] \\ $$$$\mathrm{I}_{\mathrm{n}+\mathrm{1}} \:\:\subseteq\mathrm{I}_{\mathrm{n}} \:\:\mathrm{suite}\:\mathrm{decroissante}\:\mathrm{minore} \\ $$$$\mathrm{cv}\:\mathrm{vers}\:\mathrm{lim}\:\mathrm{inf}\:\mathrm{I}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}I}_{\mathrm{n}} =\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\left.\underset{\mathrm{n}\geqslant} {\cup}\left.\mathrm{I}_{\mathrm{n}} =\mathrm{I}_{\mathrm{1}} =\right]−\mathrm{1},\mathrm{1}\right] \\ $$
Answered by aleks041103 last updated on 04/Sep/23
![∀n≥1, [0,1]⊂[−(1/n),1] ⇒[0,1]⊂∩_(n≥1) [−(1/n),1] let r<0. Then exists N∈N, s.t. (1/N)<−r⇒r<−(1/N)⇒r∉[−(1/N),1]. ⇒∀r<0, r∉∩_(n≥1) [−(1/n),1] ⇒∩_(n≥1) [−(1/n),1]=[0,1] The other is analogous.](Q196937.png)
$$\forall{n}\geqslant\mathrm{1},\:\left[\mathrm{0},\mathrm{1}\right]\subset\left[−\frac{\mathrm{1}}{{n}},\mathrm{1}\right] \\ $$$$\Rightarrow\left[\mathrm{0},\mathrm{1}\right]\subset\underset{{n}\geqslant\mathrm{1}} {\cap}\left[−\frac{\mathrm{1}}{{n}},\mathrm{1}\right] \\ $$$${let}\:{r}<\mathrm{0}.\:{Then}\:{exists}\:{N}\in\mathbb{N},\:{s}.{t}. \\ $$$$\frac{\mathrm{1}}{{N}}<−{r}\Rightarrow{r}<−\frac{\mathrm{1}}{{N}}\Rightarrow{r}\notin\left[−\frac{\mathrm{1}}{{N}},\mathrm{1}\right]. \\ $$$$\Rightarrow\forall{r}<\mathrm{0},\:{r}\notin\underset{{n}\geqslant\mathrm{1}} {\cap}\left[−\frac{\mathrm{1}}{{n}},\mathrm{1}\right] \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\cap}\left[−\frac{\mathrm{1}}{{n}},\mathrm{1}\right]=\left[\mathrm{0},\mathrm{1}\right] \\ $$$${The}\:{other}\:{is}\:{analogous}. \\ $$
