Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 196893 by hardmath last updated on 02/Sep/23

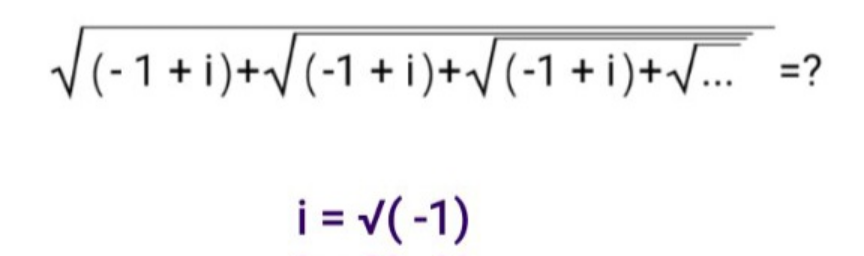
Answered by Rasheed.Sindhi last updated on 02/Sep/23

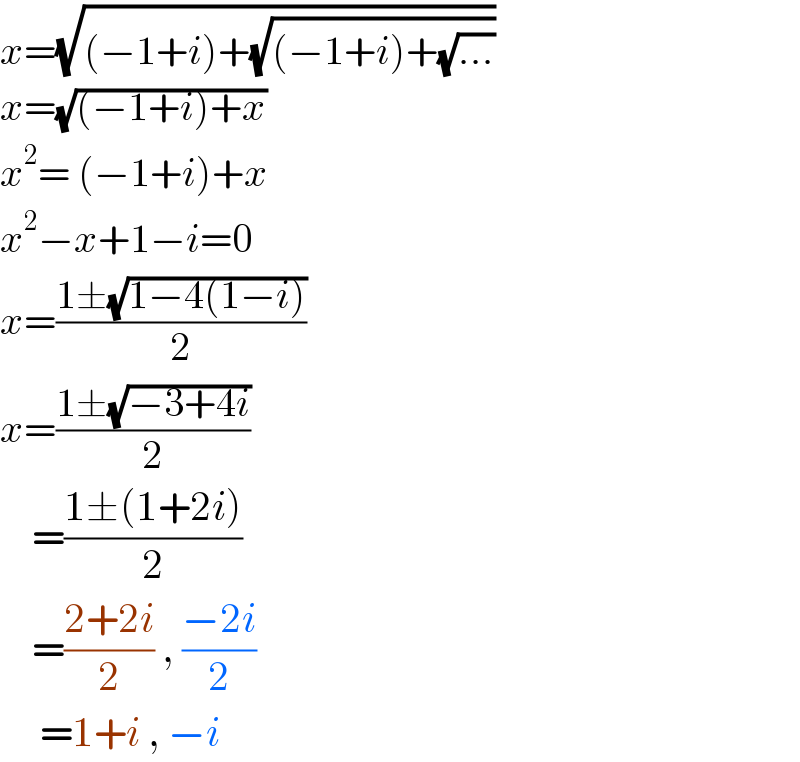
x=(√((−1+i)+(√((−1+i)+(√(...)))))) x=(√((−1+i)+x)) x^2 = (−1+i)+x x^2 −x+1−i=0 x=((1±(√(1−4(1−i))))/2) x=((1±(√(−3+4i)))/2) =((1±(1+2i))/2) =((2+2i)/2) , ((−2i)/2) =1+i , −i

$${x}=\sqrt{\left(−\mathrm{1}+{i}\right)+\sqrt{\left(−\mathrm{1}+{i}\right)+\sqrt{...}}}\: \\ $$$${x}=\sqrt{\left(−\mathrm{1}+{i}\right)+{x}}\: \\ $$$${x}^{\mathrm{2}} =\:\left(−\mathrm{1}+{i}\right)+{x} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}−{i}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}\left(\mathrm{1}−{i}\right)}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{1}\pm\sqrt{−\mathrm{3}+\mathrm{4}{i}}}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}\pm\left(\mathrm{1}+\mathrm{2}{i}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{2}+\mathrm{2}{i}}{\mathrm{2}}\:,\:\frac{−\mathrm{2}{i}}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{1}+{i}\:,\:−{i} \\ $$

Commented by BaliramKumar last updated on 02/Sep/23

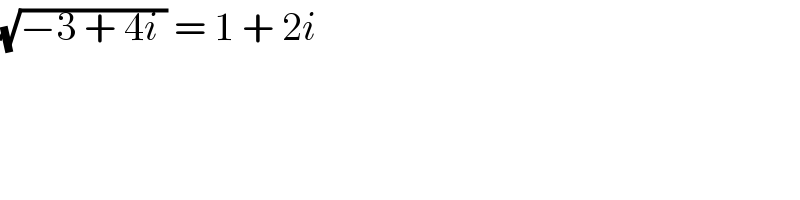
(√(−3 + 4i )) = 1 + 2i

$$\sqrt{−\mathrm{3}\:+\:\mathrm{4}{i}\:}\:=\:\mathrm{1}\:+\:\mathrm{2}{i} \\ $$

Commented by Rasheed.Sindhi last updated on 02/Sep/23

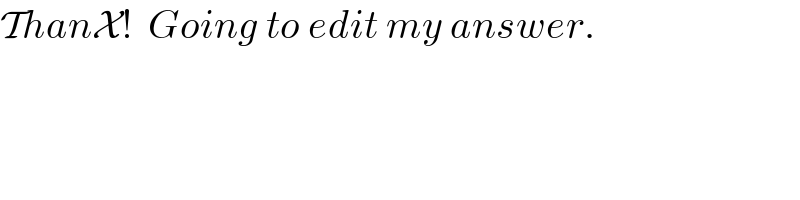
ThanX! Going to edit my answer.

$$\mathcal{T}{han}\mathcal{X}!\:\:{Going}\:{to}\:{edit}\:{my}\:{answer}. \\ $$

Commented by hardmath last updated on 05/Sep/23

thank you so much professor

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{professor} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com