Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 196886 by Amidip last updated on 02/Sep/23

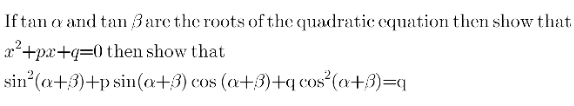
Answered by MM42 last updated on 02/Sep/23

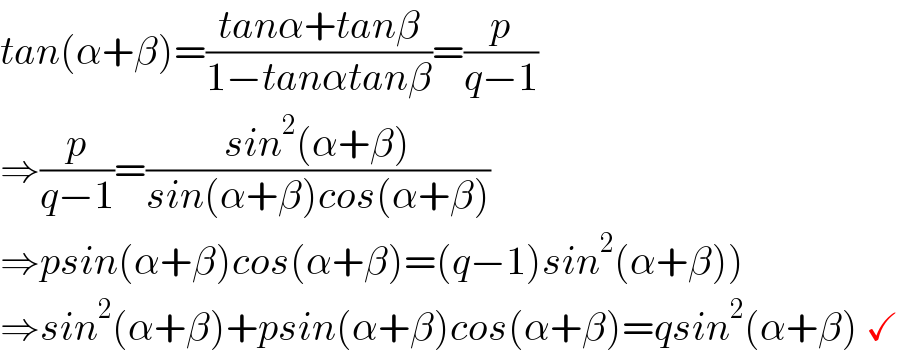
tan(α+β)=((tanα+tanβ)/(1−tanαtanβ))=(p/(q−1)) ⇒(p/(q−1))=((sin^2 (α+β))/(sin(α+β)cos(α+β))) ⇒psin(α+β)cos(α+β)=(q−1)sin^2 (α+β)) ⇒sin^2 (α+β)+psin(α+β)cos(α+β)=qsin^2 (α+β) ✓

$${tan}\left(\alpha+\beta\right)=\frac{{tan}\alpha+{tan}\beta}{\mathrm{1}−{tan}\alpha{tan}\beta}=\frac{{p}}{{q}−\mathrm{1}} \\ $$$$\Rightarrow\frac{{p}}{{q}−\mathrm{1}}=\frac{{sin}^{\mathrm{2}} \left(\alpha+\beta\right)}{{sin}\left(\alpha+\beta\right){cos}\left(\alpha+\beta\right)} \\ $$$$\left.\Rightarrow{psin}\left(\alpha+\beta\right){cos}\left(\alpha+\beta\right)=\left({q}−\mathrm{1}\right){sin}^{\mathrm{2}} \left(\alpha+\beta\right)\right) \\ $$$$\Rightarrow{sin}^{\mathrm{2}} \left(\alpha+\beta\right)+{psin}\left(\alpha+\beta\right){cos}\left(\alpha+\beta\right)={qsin}^{\mathrm{2}} \left(\alpha+\beta\right)\:\checkmark \\ $$

Answered by HeferH last updated on 02/Sep/23

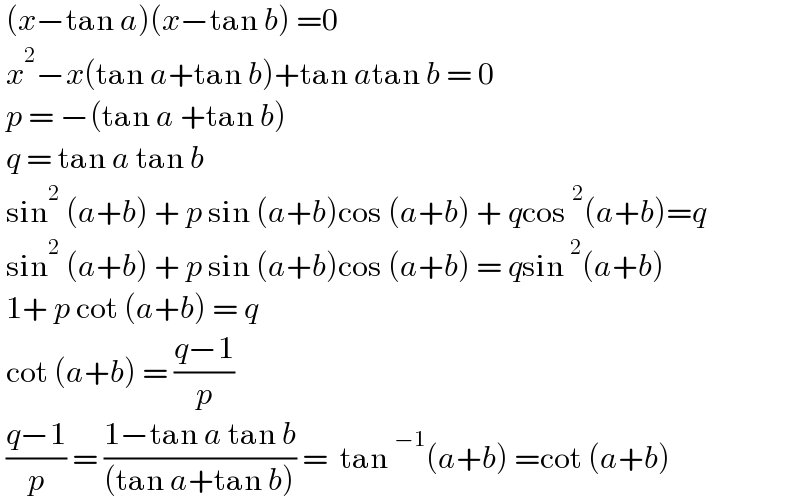
(x−tan a)(x−tan b) =0 x^2 −x(tan a+tan b)+tan atan b = 0 p = −(tan a +tan b) q = tan a tan b sin^2 (a+b) + p sin (a+b)cos (a+b) + qcos^2 (a+b)=q sin^2 (a+b) + p sin (a+b)cos (a+b) = qsin^2 (a+b) 1+ p cot (a+b) = q cot (a+b) = ((q−1)/p) ((q−1)/p) = ((1−tan a tan b)/((tan a+tan b))) = tan^(−1) (a+b) =cot (a+b)

$$\:\left({x}−\mathrm{tan}\:{a}\right)\left({x}−\mathrm{tan}\:{b}\right)\:=\mathrm{0} \\ $$$$\:{x}^{\mathrm{2}} −{x}\left(\mathrm{tan}\:{a}+\mathrm{tan}\:{b}\right)+\mathrm{tan}\:{a}\mathrm{tan}\:{b}\:=\:\mathrm{0} \\ $$$$\:{p}\:=\:−\left(\mathrm{tan}\:{a}\:+\mathrm{tan}\:{b}\right) \\ $$$$\:{q}\:=\:\mathrm{tan}\:{a}\:\mathrm{tan}\:{b}\: \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \:\left({a}+{b}\right)\:+\:{p}\:\mathrm{sin}\:\left({a}+{b}\right)\mathrm{cos}\:\left({a}+{b}\right)\:+\:{q}\mathrm{cos}\:^{\mathrm{2}} \left({a}+{b}\right)={q} \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \:\left({a}+{b}\right)\:+\:{p}\:\mathrm{sin}\:\left({a}+{b}\right)\mathrm{cos}\:\left({a}+{b}\right)\:=\:{q}\mathrm{sin}\:^{\mathrm{2}} \left({a}+{b}\right) \\ $$$$\:\mathrm{1}+\:{p}\:\mathrm{cot}\:\left({a}+{b}\right)\:=\:{q} \\ $$$$\:\mathrm{cot}\:\left({a}+{b}\right)\:=\:\frac{{q}−\mathrm{1}}{{p}} \\ $$$$\:\frac{{q}−\mathrm{1}}{{p}}\:=\:\frac{\mathrm{1}−\mathrm{tan}\:{a}\:\mathrm{tan}\:{b}}{\left(\mathrm{tan}\:{a}+\mathrm{tan}\:{b}\right)}\:=\:\:\mathrm{tan}\:^{−\mathrm{1}} \left({a}+{b}\right)\:=\mathrm{cot}\:\left({a}+{b}\right)\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com