Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 196806 by cortano12 last updated on 01/Sep/23

$$\:\:\:\:\:\cancel{\underline{\underbrace{ }}} \\ $$

Answered by dimentri last updated on 01/Sep/23

= lim_(x→0) ((x^(1/6) (2−2x)^(1/6) −x)/(2x −x ((1/(1+((x^3 +1))^(1/3) + (((x^3 +1)^2 ))^(1/3) )))^(1/3) )) = lim_(x→0) (((2−2x)^(1/6) −x^(5/6) )/(x^(5/6) (2−((1/(1+ ((x^3 +))^(1/3) +(((x^3 +1)^2 ))^(1/3) )))^(1/3) )) = ∞

$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{1}/\mathrm{6}} \left(\mathrm{2}−\mathrm{2}{x}\right)^{\mathrm{1}/\mathrm{6}} −{x}}{\mathrm{2}{x}\:−{x}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{1}+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{1}}+\:\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }}}}\: \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}−\mathrm{2}{x}\right)^{\mathrm{1}/\mathrm{6}} −{x}^{\mathrm{5}/\mathrm{6}} }{{x}^{\mathrm{5}/\mathrm{6}} \:\left(\mathrm{2}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{1}+\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +}\:+\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }}}\right.} \\ $$$$\:\:=\:\infty \\ $$

Commented by jabarsing last updated on 02/Sep/23

L^+ (0): +∞ L^− (0): Not Exist

$${L}^{+} \left(\mathrm{0}\right):\:+\infty \\ $$$${L}^{−} \left(\mathrm{0}\right):\:{Not}\:{Exist} \\ $$

Answered by jabarsing last updated on 01/Sep/23

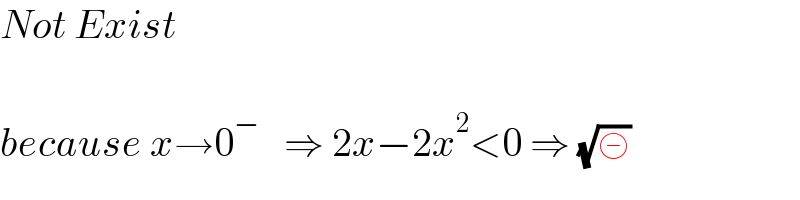
Not Exist because x→0^− ⇒ 2x−2x^2 <0 ⇒ (√⊝)

$${Not}\:{Exist} \\ $$$$ \\ $$$${because}\:{x}\rightarrow\mathrm{0}^{−} \:\:\:\Rightarrow\:\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\:\sqrt{\circleddash}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com