Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 196770 by Amidip last updated on 31/Aug/23

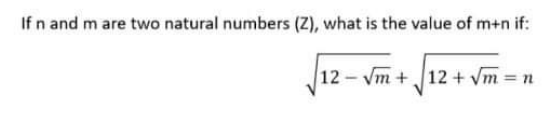
Commented by Frix last updated on 31/Aug/23

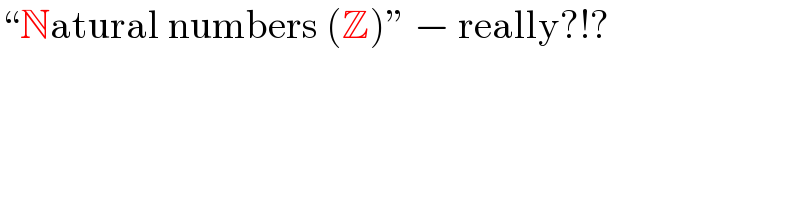
“Natural numbers (Z)” − really?!?

$$``\mathbb{N}\mathrm{atural}\:\mathrm{numbers}\:\left(\mathbb{Z}\right)''\:−\:\mathrm{really}?!? \\ $$

Commented by Frix last updated on 31/Aug/23

This has been answered. Question 196637

$$\mathrm{This}\:\mathrm{has}\:\mathrm{been}\:\mathrm{answered}. \\ $$$$\mathrm{Question}\:\mathrm{196637} \\ $$

Answered by mr W last updated on 31/Aug/23

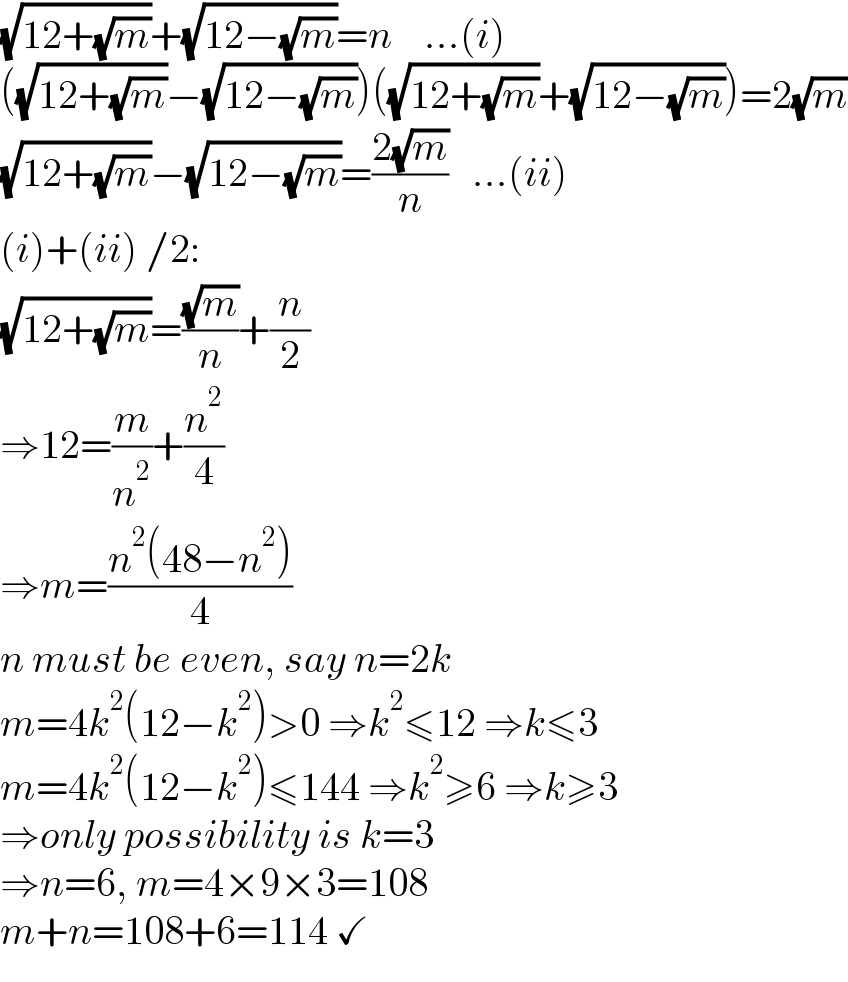
(√(12+(√m)))+(√(12−(√m)))=n ...(i) ((√(12+(√m)))−(√(12−(√m))))((√(12+(√m)))+(√(12−(√m))))=2(√m) (√(12+(√m)))−(√(12−(√m)))=((2(√m))/n) ...(ii) (i)+(ii) /2: (√(12+(√m)))=((√m)/n)+(n/2) ⇒12=(m/n^2 )+(n^2 /4) ⇒m=((n^2 (48−n^2 ))/4) n must be even, say n=2k m=4k^2 (12−k^2 )>0 ⇒k^2 ≤12 ⇒k≤3 m=4k^2 (12−k^2 )≤144 ⇒k^2 ≥6 ⇒k≥3 ⇒only possibility is k=3 ⇒n=6, m=4×9×3=108 m+n=108+6=114 ✓

$$\sqrt{\mathrm{12}+\sqrt{{m}}}+\sqrt{\mathrm{12}−\sqrt{{m}}}={n}\:\:\:\:...\left({i}\right) \\ $$$$\left(\sqrt{\mathrm{12}+\sqrt{{m}}}−\sqrt{\mathrm{12}−\sqrt{{m}}}\right)\left(\sqrt{\mathrm{12}+\sqrt{{m}}}+\sqrt{\mathrm{12}−\sqrt{{m}}}\right)=\mathrm{2}\sqrt{{m}} \\ $$$$\sqrt{\mathrm{12}+\sqrt{{m}}}−\sqrt{\mathrm{12}−\sqrt{{m}}}=\frac{\mathrm{2}\sqrt{{m}}}{{n}}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\:/\mathrm{2}: \\ $$$$\sqrt{\mathrm{12}+\sqrt{{m}}}=\frac{\sqrt{{m}}}{{n}}+\frac{{n}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}=\frac{{m}}{{n}^{\mathrm{2}} }+\frac{{n}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{m}=\frac{{n}^{\mathrm{2}} \left(\mathrm{48}−{n}^{\mathrm{2}} \right)}{\mathrm{4}} \\ $$$${n}\:{must}\:{be}\:{even},\:{say}\:{n}=\mathrm{2}{k} \\ $$$${m}=\mathrm{4}{k}^{\mathrm{2}} \left(\mathrm{12}−{k}^{\mathrm{2}} \right)>\mathrm{0}\:\Rightarrow{k}^{\mathrm{2}} \leqslant\mathrm{12}\:\Rightarrow{k}\leqslant\mathrm{3} \\ $$$${m}=\mathrm{4}{k}^{\mathrm{2}} \left(\mathrm{12}−{k}^{\mathrm{2}} \right)\leqslant\mathrm{144}\:\Rightarrow{k}^{\mathrm{2}} \geqslant\mathrm{6}\:\Rightarrow{k}\geqslant\mathrm{3} \\ $$$$\Rightarrow{only}\:{possibility}\:{is}\:{k}=\mathrm{3} \\ $$$$\Rightarrow{n}=\mathrm{6},\:{m}=\mathrm{4}×\mathrm{9}×\mathrm{3}=\mathrm{108} \\ $$$${m}+{n}=\mathrm{108}+\mathrm{6}=\mathrm{114}\:\checkmark \\ $$

Commented by Frix last updated on 01/Sep/23

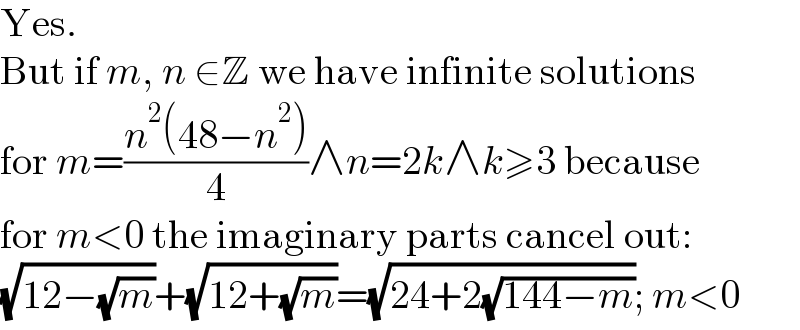
Yes. But if m, n ∈Z we have infinite solutions for m=((n^2 (48−n^2 ))/4)∧n=2k∧k≥3 because for m<0 the imaginary parts cancel out: (√(12−(√m)))+(√(12+(√m)))=(√(24+2(√(144−m)))); m<0

$$\mathrm{Yes}. \\ $$$$\mathrm{But}\:\mathrm{if}\:{m},\:{n}\:\in\mathbb{Z}\:\mathrm{we}\:\mathrm{have}\:\mathrm{infinite}\:\mathrm{solutions} \\ $$$$\mathrm{for}\:{m}=\frac{{n}^{\mathrm{2}} \left(\mathrm{48}−{n}^{\mathrm{2}} \right)}{\mathrm{4}}\wedge{n}=\mathrm{2}{k}\wedge{k}\geqslant\mathrm{3}\:\mathrm{because} \\ $$$$\mathrm{for}\:{m}<\mathrm{0}\:\mathrm{the}\:\mathrm{imaginary}\:\mathrm{parts}\:\mathrm{cancel}\:\mathrm{out}: \\ $$$$\sqrt{\mathrm{12}−\sqrt{{m}}}+\sqrt{\mathrm{12}+\sqrt{{m}}}=\sqrt{\mathrm{24}+\mathrm{2}\sqrt{\mathrm{144}−{m}}};\:{m}<\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com