
Question Number 196735 by sonukgindia last updated on 30/Aug/23
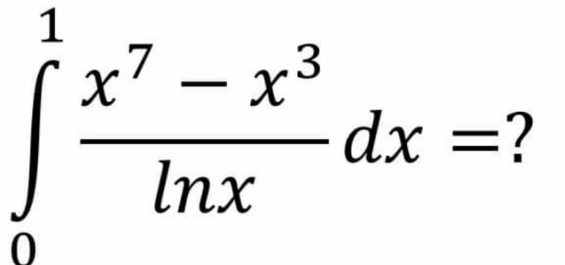
Answered by qaz last updated on 31/Aug/23
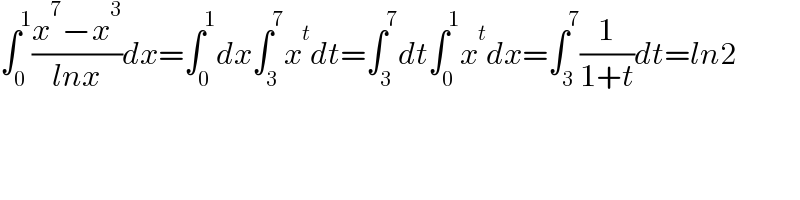
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{7}} −{x}^{\mathrm{3}} }{{lnx}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {dx}\int_{\mathrm{3}} ^{\mathrm{7}} {x}^{{t}} {dt}=\int_{\mathrm{3}} ^{\mathrm{7}} {dt}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{t}} {dx}=\int_{\mathrm{3}} ^{\mathrm{7}} \frac{\mathrm{1}}{\mathrm{1}+{t}}{dt}={ln}\mathrm{2} \\ $$
Answered by leodera last updated on 05/Sep/23
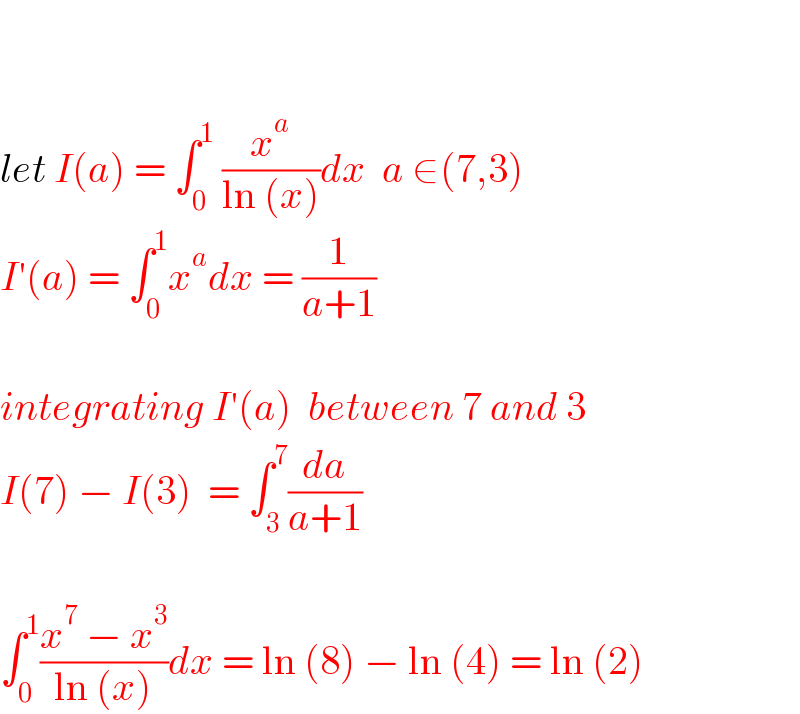
$$ \\ $$$$ \\ $$$${let}\:{I}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{a}} }{\mathrm{ln}\:\left({x}\right)}{dx}\:\:{a}\:\in\left(\mathrm{7},\mathrm{3}\right) \\ $$$${I}'\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} {dx}\:=\:\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$ \\ $$$${integrating}\:{I}'\left({a}\right)\:\:{between}\:\mathrm{7}\:{and}\:\mathrm{3} \\ $$$${I}\left(\mathrm{7}\right)\:−\:{I}\left(\mathrm{3}\right)\:\:=\:\int_{\mathrm{3}} ^{\mathrm{7}} \frac{{da}}{{a}+\mathrm{1}} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{7}} \:−\:{x}^{\mathrm{3}} }{\mathrm{ln}\:\left({x}\right)}{dx}\:=\:\mathrm{ln}\:\left(\mathrm{8}\right)\:−\:\mathrm{ln}\:\left(\mathrm{4}\right)\:=\:\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$
