
Question Number 196714 by mr W last updated on 30/Aug/23
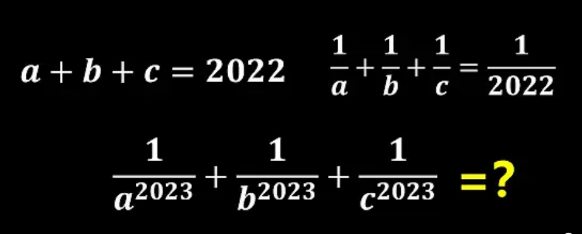
Answered by som(math1967) last updated on 30/Aug/23
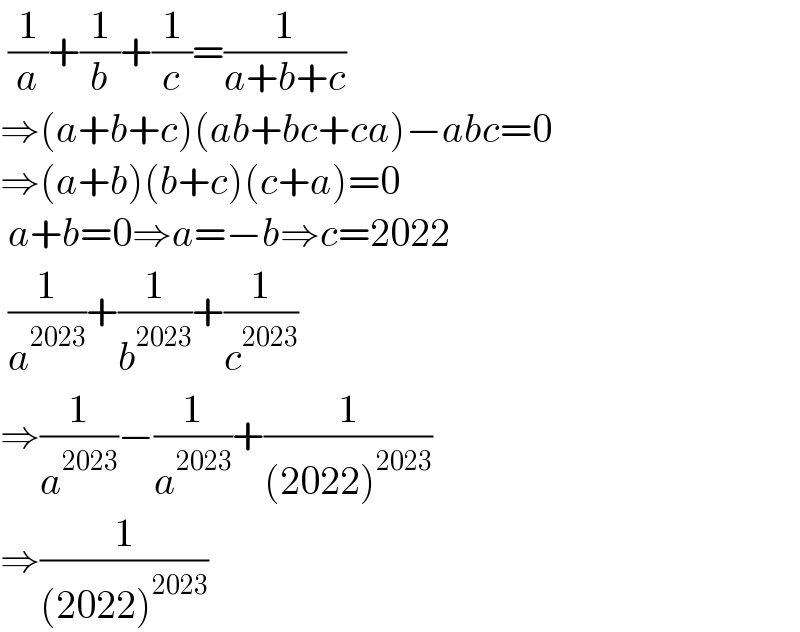
$$\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{{a}+{b}+{c}} \\ $$$$\Rightarrow\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ca}\right)−{abc}=\mathrm{0} \\ $$$$\Rightarrow\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right)=\mathrm{0} \\ $$$$\:{a}+{b}=\mathrm{0}\Rightarrow{a}=−{b}\Rightarrow{c}=\mathrm{2022} \\ $$$$\:\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2023}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{\left(\mathrm{2022}\right)^{\mathrm{2023}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{2022}\right)^{\mathrm{2023}} } \\ $$
Commented by mr W last updated on 30/Aug/23

$${very}\:{nice}! \\ $$
Answered by Rasheed.Sindhi last updated on 30/Aug/23

$${a}+{b}+{c}=\mathrm{2022},\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{\mathrm{2022}} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2023}} }=? \\ $$$$\frac{{a}+{b}}{{ab}}=\frac{\mathrm{1}}{\mathrm{2022}}−\frac{\mathrm{1}}{{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2022}}−\frac{\mathrm{1}}{\mathrm{2022}−\left({a}+{b}\right)} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{2022}−\left({a}+{b}\right)−\mathrm{2022}}{\mathrm{2022}\left(\:\mathrm{2022}−\left({a}+{b}\right)\:\right)} \\ $$$$\:\:\:\:\:\:=\frac{{a}+{b}}{\mathrm{2022}\left(\left({a}+{b}\right)−\:\mathrm{2022}\right)} \\ $$$$\frac{{a}+{b}}{{ab}}−\frac{{a}+{b}}{\mathrm{2022}\left(\left({a}+{b}\right)−\:\mathrm{2022}\right)}=\mathrm{0} \\ $$$$\left({a}+{b}\right)\left(\frac{\mathrm{1}}{{ab}}−\frac{\mathrm{1}}{\mathrm{2022}\left(\left({a}+{b}\right)−\:\mathrm{2022}\right)}\right)=\mathrm{0} \\ $$$${a}=−{b}\:^{\bigstar} \:\mid\:\frac{\mathrm{1}}{\mathrm{2022}\left(\left({a}+{b}\right)−\:\mathrm{20222}\right)}=\frac{\mathrm{1}}{{ab}} \\ $$$$\mathrm{2022}\left({a}+{b}\right)−\mathrm{2022}^{\mathrm{2}} −{ab}=\mathrm{0} \\ $$$$\left(\mathrm{2022}−{a}\right)\left({b}−\mathrm{2022}\right)=\mathrm{0} \\ $$$$\:\:{a}=\mathrm{2022}\:\mid\:{b}=\mathrm{2022} \\ $$$${a}+{b}+{c}=\mathrm{2022} \\ $$$$\mathrm{2022}+\mathrm{2022}+{c}=\mathrm{2022} \\ $$$${c}=−\mathrm{2022} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2023}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }+\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }+\frac{\mathrm{1}}{\left(−\mathrm{2022}\right)^{\mathrm{2023}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }+\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }−\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }\:\checkmark \\ $$$$\:^{\bigstar} \:{a}=−{b} \\ $$$$\:\:\:\:\:{a}+{b}+{c}=\mathrm{2022}\Rightarrow−{b}+{b}+{c}=\mathrm{2022} \\ $$$$\Rightarrow{c}=\mathrm{2022} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2023}} } \\ $$$$\frac{\mathrm{1}}{\left(−{b}\right)^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{\left(\mathrm{2022}\right)^{\mathrm{2023}} } \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2022}\right)^{\mathrm{2023}} }\:\checkmark \\ $$$$ \\ $$
Commented by mr W last updated on 30/Aug/23

$${thanks}! \\ $$
Answered by Rasheed.Sindhi last updated on 30/Aug/23

$${a}+{b}+{c}=\mathrm{2022}\:,\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{\mathrm{2022}} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2023}} }=? \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{\mathrm{2022}} \\ $$$$\Rightarrow{ab}+{bc}+{ca}=\frac{{abc}}{\mathrm{2022}} \\ $$$${Let}\:{a},{b},{c}\:{are}\:{roots}\:{of}\:{an}\:{equation}. \\ $$$${Equation}\:{will}\:{be}: \\ $$$${x}^{\mathrm{3}} −\left({a}+{b}+{c}\right){x}^{\mathrm{2}} +\left({ab}+{bc}+{ca}\right){x}−{abc}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{2022}{x}^{\mathrm{2}} +\left(\frac{{abc}}{\mathrm{2022}}\right){x}−{abc}=\mathrm{0} \\ $$$$\mathrm{2022}{x}^{\mathrm{3}} −\mathrm{2022}^{\mathrm{2}} {x}^{\mathrm{2}} +{abcx}−\mathrm{2022}{abc}=\mathrm{0} \\ $$$$\mathrm{2022}{x}^{\mathrm{2}} \left({x}−\mathrm{2022}\right)+{abc}\left({x}−\mathrm{2022}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{2022}\right)\left(\mathrm{2022}{x}^{\mathrm{2}} +{abc}\right)=\mathrm{0} \\ $$$${x}=\mathrm{2022}\:\mid\:\mathrm{2022}{x}^{\mathrm{2}} +{abc}=\mathrm{0} \\ $$$$\:{let}\:{a}=\mathrm{2022}\:\mid\:\mathrm{2022}{x}^{\mathrm{2}} +\mathrm{2022}{bc}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{x}^{\mathrm{2}} =−{bc} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{x}=\pm\sqrt{−{bc}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{Let}\:\:{b}=\sqrt{−{bc}}\:\&\:{c}=−\sqrt{−{bc}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{b}+{c}=\mathrm{0}\Rightarrow{c}=−{b} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2023}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2023}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }+\frac{\mathrm{1}}{\left({b}\right)^{\mathrm{2023}} }+\frac{\mathrm{1}}{\left(−{b}\right)^{\mathrm{2023}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }+\cancel{\frac{\mathrm{1}}{\left({b}\right)^{\mathrm{2023}} }}−\cancel{\frac{\mathrm{1}}{\left({b}\right)^{\mathrm{2023}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2023}} }\:\checkmark \\ $$
