
Question Number 196688 by cortano12 last updated on 29/Aug/23
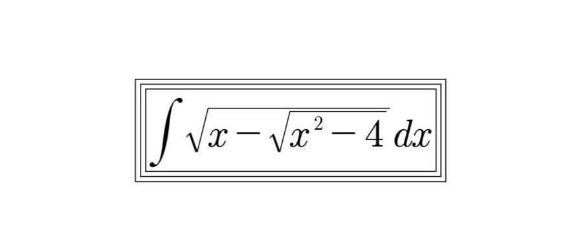
Answered by Frix last updated on 29/Aug/23
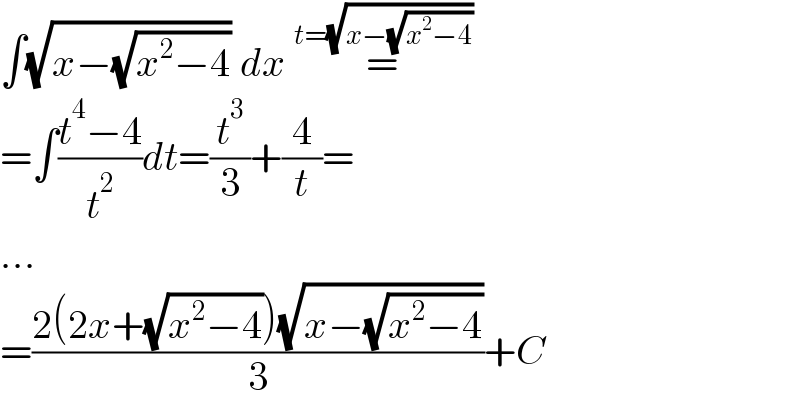
$$\int\sqrt{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}\:{dx}\:\overset{{t}=\sqrt{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}} {=} \\ $$$$=\int\frac{{t}^{\mathrm{4}} −\mathrm{4}}{{t}^{\mathrm{2}} }{dt}=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{4}}{{t}}= \\ $$$$... \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\right)\sqrt{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}}{\mathrm{3}}+{C} \\ $$
Commented by cortano12 last updated on 30/Aug/23

$$\mathrm{Euler}'\mathrm{s}\:\mathrm{Subtitution} \\ $$
