
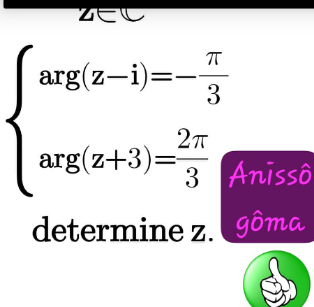
Question Number 196667 by ERLY last updated on 29/Aug/23
Answered by Frix last updated on 29/Aug/23

$$\mathrm{No}\:\mathrm{solution}. \\ $$
Answered by Phelaire last updated on 29/Aug/23

$${pas}\:{de}\:{solution} \\ $$
Answered by Frix last updated on 29/Aug/23

$$\mathrm{We}\:\mathrm{can}\:\mathrm{shift}\:\mathrm{the}\:\mathrm{coordinate}\:\mathrm{system}\:\mathrm{by}\:−{z} \\ $$$$\Rightarrow \\ $$$${z}=\mathrm{0}+\mathrm{0i} \\ $$$$\mathrm{Now}\:\mathrm{intersect}\:\mathrm{the}\:\mathrm{lines} \\ $$$${L}_{\mathrm{1}} :\:{y}={ax}+{b};\:\left(\mathrm{0},\:−\mathrm{1}\right)\in{L}_{\mathrm{1}} ;\:{a}=\mathrm{tan}\:−\frac{\pi}{\mathrm{3}} \\ $$$${L}_{\mathrm{2}} :\:{y}={cx}+{d};\:\left(\mathrm{3},\:\mathrm{0}\right)\in{L}_{\mathrm{2}} ;\:{c}=\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${L}_{\mathrm{1}} :\:{y}=−\sqrt{\mathrm{3}}{x}−\mathrm{1} \\ $$$${L}_{\mathrm{2}} :\:{y}=−\sqrt{\mathrm{3}}{x}+\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$\mathrm{These}\:\mathrm{lines}\:\mathrm{are}\:\mathrm{parallel}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$
Commented by ERLY last updated on 01/Sep/23

$${expliQuez} \\ $$
