Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 196659 by sonukgindia last updated on 29/Aug/23

Commented by Rasheed.Sindhi last updated on 29/Aug/23

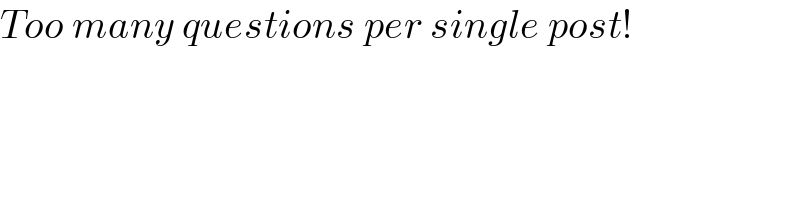
Too many questions per single post!

$${Too}\:{many}\:{questions}\:{per}\:{single}\:{post}! \\ $$

Commented by Rasheed.Sindhi last updated on 29/Aug/23

Q#8 2058000, 2058343, 2058686

$${Q}#\mathrm{8} \\ $$$$\mathrm{2058000},\:\mathrm{2058343},\:\mathrm{2058686} \\ $$

Commented by deleteduser1 last updated on 29/Aug/23

[V.9.]Last digit (−1)×1010+(1)×1010=0 (Ω/(10))≡(0/(10))≡0(mod 10)⇒Last two digits=00

$$\left[{V}.\mathrm{9}.\right]{Last}\:{digit}\:\left(−\mathrm{1}\right)×\mathrm{1010}+\left(\mathrm{1}\right)×\mathrm{1010}=\mathrm{0} \\ $$$$\frac{\Omega}{\mathrm{10}}\equiv\frac{\mathrm{0}}{\mathrm{10}}\equiv\mathrm{0}\left({mod}\:\mathrm{10}\right)\Rightarrow{Last}\:{two}\:{digits}=\mathrm{00} \\ $$

Commented by deleteduser1 last updated on 29/Aug/23

[V.7.] Ω_1 −Ω_2 =(36^1 −25^1 )+(36^2 −25^2 )+...+(36^n −25^n ) 36^n −25^n ≡3^n −3^n ≡^(11) 0⇒Ω_1 −Ω_2 ≡^(11) 0

$$\left[{V}.\mathrm{7}.\right]\:\Omega_{\mathrm{1}} −\Omega_{\mathrm{2}} =\left(\mathrm{36}^{\mathrm{1}} −\mathrm{25}^{\mathrm{1}} \right)+\left(\mathrm{36}^{\mathrm{2}} −\mathrm{25}^{\mathrm{2}} \right)+...+\left(\mathrm{36}^{{n}} −\mathrm{25}^{{n}} \right) \\ $$$$\mathrm{36}^{{n}} −\mathrm{25}^{{n}} \equiv\mathrm{3}^{{n}} −\mathrm{3}^{{n}} \overset{\mathrm{11}} {\equiv}\mathrm{0}\Rightarrow\Omega_{\mathrm{1}} −\Omega_{\mathrm{2}} \overset{\mathrm{11}} {\equiv}\mathrm{0} \\ $$

Answered by Rasheed.Sindhi last updated on 29/Aug/23

(1/(a+1))+(2/(b+1))+(3/(c+1))+(4/(d+1))=1 (a/(a+1))+((2b)/(b+1))+((3c)/(c+1))+((4d)/(d+1))=? −.−.−.−.−.−.−.−.−.−.−.−.−.−.−.− ▶(1/(a+1))+1+(2/(b+1))+2+(3/(c+1))+3+(4/(d+1))+4=1+10 ▶((a+2)/(a+1))+((2b+4)/(b+1))+((3c+6)/(c+1))+((4d+8)/(d+1))=11 ▶((a/(a+1))+(2/(a+1)))+(((2b)/(b+1))+(4/(b+1))) +(((3c)/(c+1))+(6/(c+1)))+(((4d)/(d+1))+(8/(d+1)))=11 ▶((a/(a+1))+((2b)/(b+1))+((3c)/(c+1))+((4d)/(d+1))) +((2/(a+1))+(4/(b+1))+(6/(c+1))+(8/(d+1)))=11 ▶((a/(a+1))+((2b)/(b+1))+((3c)/(c+1))+((4d)/(d+1))) +2((1/(a+1))+(2/(b+1))+(3/(c+1))+(4/(d+1)))=11 ▶((a/(a+1))+((2b)/(b+1))+((3c)/(c+1))+((4d)/(d+1))) +2(1)=11 ▶(a/(a+1))+((2b)/(b+1))+((3c)/(c+1))+((4d)/(d+1))=11−2=9✓

$$\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{2}}{{b}+\mathrm{1}}+\frac{\mathrm{3}}{{c}+\mathrm{1}}+\frac{\mathrm{4}}{{d}+\mathrm{1}}=\mathrm{1} \\ $$$$\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}}{{d}+\mathrm{1}}=? \\ $$$$−.−.−.−.−.−.−.−.−.−.−.−.−.−.−.− \\ $$$$\blacktriangleright\frac{\mathrm{1}}{{a}+\mathrm{1}}+\mathrm{1}+\frac{\mathrm{2}}{{b}+\mathrm{1}}+\mathrm{2}+\frac{\mathrm{3}}{{c}+\mathrm{1}}+\mathrm{3}+\frac{\mathrm{4}}{{d}+\mathrm{1}}+\mathrm{4}=\mathrm{1}+\mathrm{10} \\ $$$$\blacktriangleright\frac{{a}+\mathrm{2}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}+\mathrm{4}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}+\mathrm{6}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}+\mathrm{8}}{{d}+\mathrm{1}}=\mathrm{11} \\ $$$$\blacktriangleright\left(\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}}{{a}+\mathrm{1}}\right)+\left(\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{4}}{{b}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:+\left(\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{6}}{{c}+\mathrm{1}}\right)+\left(\frac{\mathrm{4}{d}}{{d}+\mathrm{1}}+\frac{\mathrm{8}}{{d}+\mathrm{1}}\right)=\mathrm{11} \\ $$$$\blacktriangleright\left(\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}}{{d}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:+\left(\frac{\mathrm{2}}{{a}+\mathrm{1}}+\frac{\mathrm{4}}{{b}+\mathrm{1}}+\frac{\mathrm{6}}{{c}+\mathrm{1}}+\frac{\mathrm{8}}{{d}+\mathrm{1}}\right)=\mathrm{11} \\ $$$$\blacktriangleright\left(\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}}{{d}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:+\mathrm{2}\left(\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{2}}{{b}+\mathrm{1}}+\frac{\mathrm{3}}{{c}+\mathrm{1}}+\frac{\mathrm{4}}{{d}+\mathrm{1}}\right)=\mathrm{11} \\ $$$$\blacktriangleright\left(\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}}{{d}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left(\mathrm{1}\right)=\mathrm{11} \\ $$$$\blacktriangleright\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}}{{d}+\mathrm{1}}=\mathrm{11}−\mathrm{2}=\mathrm{9}\checkmark \\ $$$$\: \\ $$

Commented by mnjuly1970 last updated on 29/Aug/23

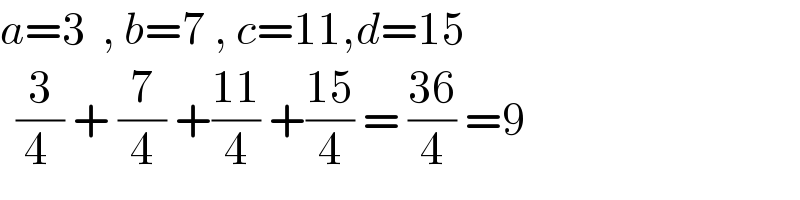
a=3 , b=7 , c=11,d=15 (3/(4 )) + (7/4) +((11)/4) +((15)/4) = ((36)/4) =9

$${a}=\mathrm{3}\:\:,\:{b}=\mathrm{7}\:,\:{c}=\mathrm{11},{d}=\mathrm{15} \\ $$$$\:\:\frac{\mathrm{3}}{\mathrm{4}\:}\:+\:\frac{\mathrm{7}}{\mathrm{4}}\:+\frac{\mathrm{11}}{\mathrm{4}}\:+\frac{\mathrm{15}}{\mathrm{4}}\:=\:\frac{\mathrm{36}}{\mathrm{4}}\:=\mathrm{9} \\ $$

Commented by Rasheed.Sindhi last updated on 29/Aug/23

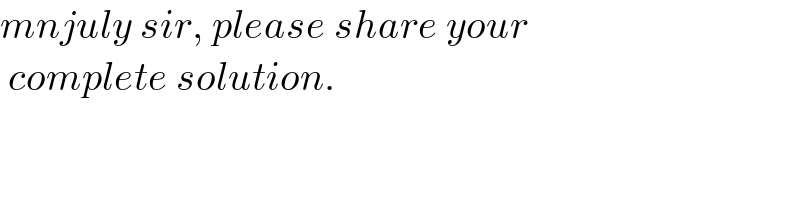
mnjuly sir, please share your complete solution.

$${mnjuly}\:{sir},\:{please}\:{share}\:{your} \\ $$$$\:{complete}\:{solution}. \\ $$

Answered by Rasheed.Sindhi last updated on 29/Aug/23

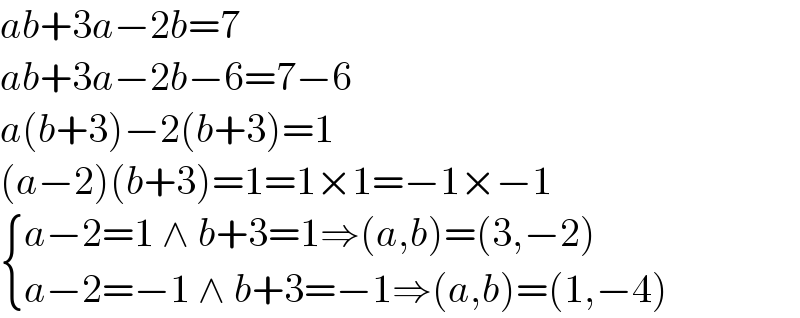
ab+3a−2b=7 ab+3a−2b−6=7−6 a(b+3)−2(b+3)=1 (a−2)(b+3)=1=1×1=−1×−1 { ((a−2=1 ∧ b+3=1⇒(a,b)=(3,−2))),((a−2=−1 ∧ b+3=−1⇒(a,b)=(1,−4))) :}

$${ab}+\mathrm{3}{a}−\mathrm{2}{b}=\mathrm{7} \\ $$$${ab}+\mathrm{3}{a}−\mathrm{2}{b}−\mathrm{6}=\mathrm{7}−\mathrm{6} \\ $$$${a}\left({b}+\mathrm{3}\right)−\mathrm{2}\left({b}+\mathrm{3}\right)=\mathrm{1} \\ $$$$\left({a}−\mathrm{2}\right)\left({b}+\mathrm{3}\right)=\mathrm{1}=\mathrm{1}×\mathrm{1}=−\mathrm{1}×−\mathrm{1} \\ $$$$\begin{cases}{{a}−\mathrm{2}=\mathrm{1}\:\wedge\:{b}+\mathrm{3}=\mathrm{1}\Rightarrow\left({a},{b}\right)=\left(\mathrm{3},−\mathrm{2}\right)}\\{{a}−\mathrm{2}=−\mathrm{1}\:\wedge\:{b}+\mathrm{3}=−\mathrm{1}\Rightarrow\left({a},{b}\right)=\left(\mathrm{1},−\mathrm{4}\right)}\end{cases} \\ $$

Answered by universe last updated on 29/Aug/23

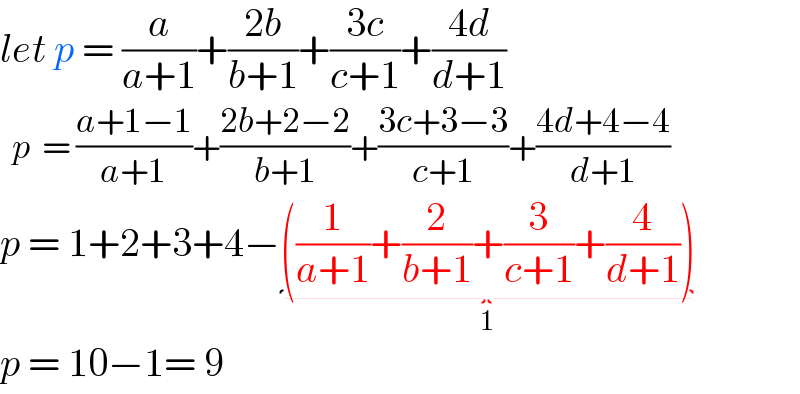
let p = (a/(a+1))+((2b)/(b+1))+((3c)/(c+1))+((4d)/(d+1)) p = ((a+1−1)/(a+1))+((2b+2−2)/(b+1))+((3c+3−3)/(c+1))+((4d+4−4)/(d+1)) p = 1+2+3+4−((1/(a+1))+(2/(b+1))+(3/(c+1))+(4/(d+1)))_(1) p = 10−1= 9

$${let}\:{p}\:=\:\frac{{a}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}}{{d}+\mathrm{1}} \\ $$$$\:\:{p}\:\:=\:\frac{{a}+\mathrm{1}−\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{2}{b}+\mathrm{2}−\mathrm{2}}{{b}+\mathrm{1}}+\frac{\mathrm{3}{c}+\mathrm{3}−\mathrm{3}}{{c}+\mathrm{1}}+\frac{\mathrm{4}{d}+\mathrm{4}−\mathrm{4}}{{d}+\mathrm{1}} \\ $$$${p}\:=\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}−\underset{\mathrm{1}} {\underbrace{\left(\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{2}}{{b}+\mathrm{1}}+\frac{\mathrm{3}}{{c}+\mathrm{1}}+\frac{\mathrm{4}}{{d}+\mathrm{1}}\right)}} \\ $$$${p}\:=\:\mathrm{10}−\mathrm{1}=\:\mathrm{9} \\ $$

Answered by Rasheed.Sindhi last updated on 29/Aug/23

Q#6 Ω_1 +Ω_2 =676 ,(Ω_1 ,Ω_2 )=169 Let Ω_1 =169m & Ω_2 =169n, where (m,n)=1 Ω_1 +Ω_2 =169m+169n=676 m+n=4 ∧ (m,n)=1 (m,n)=(1,3),(3,1) (Ω_1 ,Ω_2 )=(1×169,3×169),(3×169,1×169) =(169,507),(507,169) Note:One of the 2 figures(876 & 169) is wrong at least. I have corrected: 876^(676) .

$${Q}#\mathrm{6}\: \\ $$$$\Omega_{\mathrm{1}} +\Omega_{\mathrm{2}} =\mathrm{676}\:,\left(\Omega_{\mathrm{1}} ,\Omega_{\mathrm{2}} \right)=\mathrm{169} \\ $$$${Let}\:\Omega_{\mathrm{1}} =\mathrm{169}{m}\:\&\:\Omega_{\mathrm{2}} =\mathrm{169}{n},\:{where} \\ $$$$\left({m},{n}\right)=\mathrm{1} \\ $$$$\Omega_{\mathrm{1}} +\Omega_{\mathrm{2}} =\mathrm{169}{m}+\mathrm{169}{n}=\mathrm{676} \\ $$$${m}+{n}=\mathrm{4}\:\wedge\:\left({m},{n}\right)=\mathrm{1} \\ $$$$\left({m},{n}\right)=\left(\mathrm{1},\mathrm{3}\right),\left(\mathrm{3},\mathrm{1}\right) \\ $$$$\left(\Omega_{\mathrm{1}} ,\Omega_{\mathrm{2}} \right)=\left(\mathrm{1}×\mathrm{169},\mathrm{3}×\mathrm{169}\right),\left(\mathrm{3}×\mathrm{169},\mathrm{1}×\mathrm{169}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{169},\mathrm{507}\right),\left(\mathrm{507},\mathrm{169}\right) \\ $$$${Note}:{One}\:{of}\:{the}\:\mathrm{2}\:{figures}\left(\mathrm{876}\:\&\:\mathrm{169}\right)\:{is}\:{wrong}\:{at}\:{least}. \\ $$$${I}\:{have}\:{corrected}:\:\cancel{\overset{\mathrm{676}} {\mathrm{876}}}\:. \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 29/Aug/23

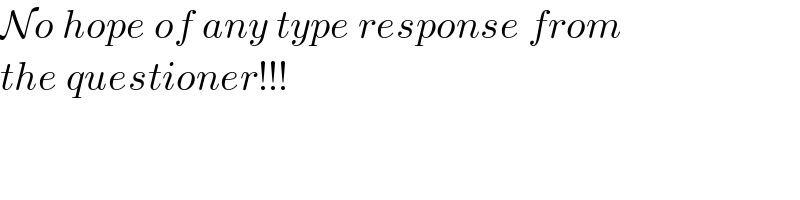
No hope of any type response from the questioner!!!

$$\mathcal{N}{o}\:{hope}\:{of}\:{any}\:{type}\:{response}\:{from} \\ $$$${the}\:{questioner}!!! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com