
Question Number 196576 by sonukgindia last updated on 27/Aug/23
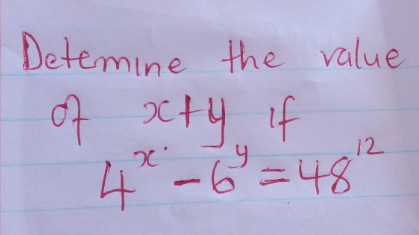
Commented by Frix last updated on 27/Aug/23
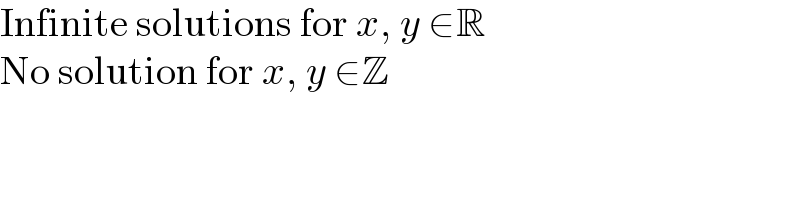
$$\mathrm{Infinite}\:\mathrm{solutions}\:\mathrm{for}\:{x},\:{y}\:\in\mathbb{R} \\ $$$$\mathrm{No}\:\mathrm{solution}\:\mathrm{for}\:{x},\:{y}\:\in\mathbb{Z} \\ $$
Answered by sniper237 last updated on 27/Aug/23
![Such numbers can′t exist!!! 4^x ≡1[3] ; 48^(12) ≡0[3]⇒ 1−6^y ≡0[3] So y=0. Then 4^x =1+48^(12) 48^(12) ≡0[2]⇒ 4^x ≡1[2]⇒x=0 But 4^0 −6^0 ≠48^(12) .](Q196593.png)
$${Such}\:{numbers}\:{can}'{t}\:{exist}!!! \\ $$$$\mathrm{4}^{{x}} \equiv\mathrm{1}\left[\mathrm{3}\right]\:;\:\mathrm{48}^{\mathrm{12}} \equiv\mathrm{0}\left[\mathrm{3}\right]\Rightarrow\:\mathrm{1}−\mathrm{6}^{{y}} \equiv\mathrm{0}\left[\mathrm{3}\right] \\ $$$${So}\:\:{y}=\mathrm{0}.\:{Then}\:\:\mathrm{4}^{{x}} =\mathrm{1}+\mathrm{48}^{\mathrm{12}} \\ $$$$\mathrm{48}^{\mathrm{12}} \equiv\mathrm{0}\left[\mathrm{2}\right]\Rightarrow\:\mathrm{4}^{{x}} \equiv\mathrm{1}\left[\mathrm{2}\right]\Rightarrow{x}=\mathrm{0} \\ $$$${But}\:\:\mathrm{4}^{\mathrm{0}} −\mathrm{6}^{\mathrm{0}} \neq\mathrm{48}^{\mathrm{12}} .\: \\ $$
Commented by deleteduser1 last updated on 27/Aug/23

$${That}'{s}\:{if}\:{x},{y}\in\mathbb{Z} \\ $$
