
Question Number 196560 by peter frank last updated on 27/Aug/23
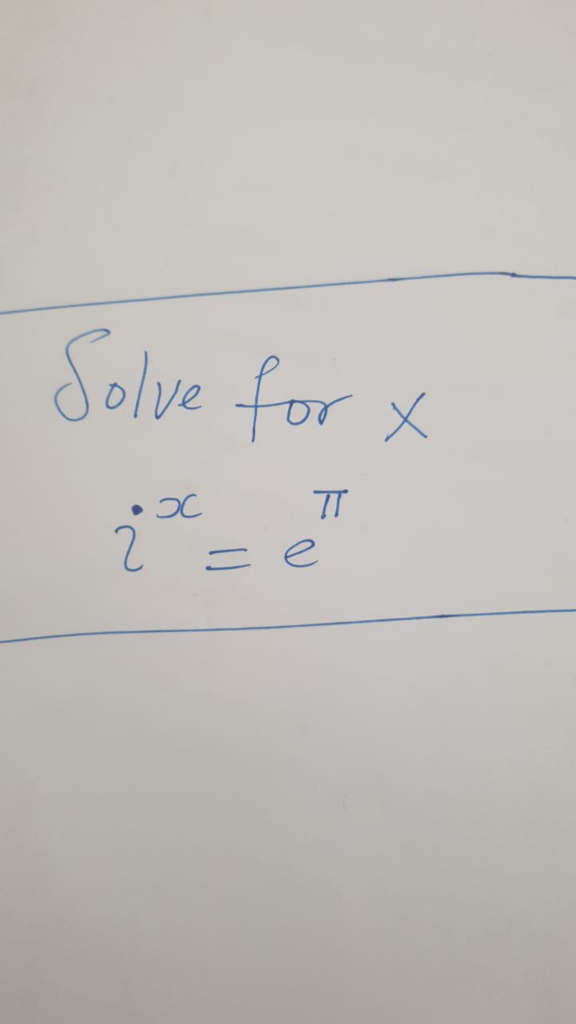
Commented by Spillover last updated on 27/Aug/23
Check your solution https://m.facebook.com/story.php?story_fbid=pfbid0QHNhoZjesQzGqy7jHAgbvRSRUx25yXHezsGoh2qHLCapd9KB4z5PFi88czsFYxZ6l&id=100084816875916&mibextid=Nif5oz
Answered by MM42 last updated on 27/Aug/23
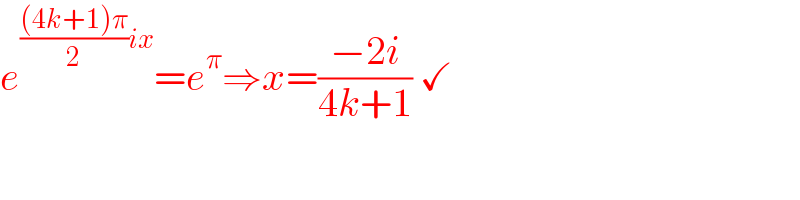
$${e}^{\frac{\left(\mathrm{4}{k}+\mathrm{1}\right)\pi}{\mathrm{2}}{ix}} ={e}^{\pi} \Rightarrow{x}=\frac{−\mathrm{2}{i}}{\mathrm{4}{k}+\mathrm{1}}\:\checkmark\: \\ $$
Commented by Frix last updated on 27/Aug/23
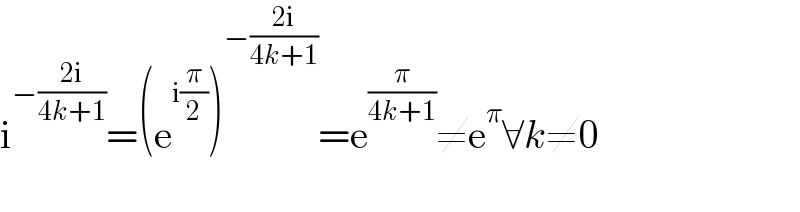
$$\mathrm{i}^{−\frac{\mathrm{2i}}{\mathrm{4}{k}+\mathrm{1}}} =\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \right)^{−\frac{\mathrm{2i}}{\mathrm{4}{k}+\mathrm{1}}} =\mathrm{e}^{\frac{\pi}{\mathrm{4}{k}+\mathrm{1}}} \neq\mathrm{e}^{\pi} \forall{k}\neq\mathrm{0} \\ $$$$ \\ $$
Commented by MM42 last updated on 28/Aug/23
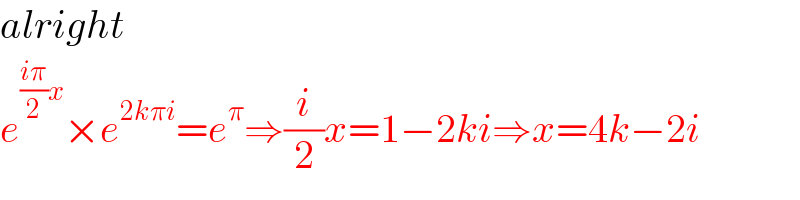
$${alright} \\ $$$${e}^{\frac{{i}\pi}{\mathrm{2}}{x}} ×{e}^{\mathrm{2}{k}\pi{i}} ={e}^{\pi} \Rightarrow\frac{{i}}{\mathrm{2}}{x}=\mathrm{1}−\mathrm{2}{ki}\Rightarrow{x}=\mathrm{4}{k}−\mathrm{2}{i} \\ $$
Answered by Frix last updated on 27/Aug/23
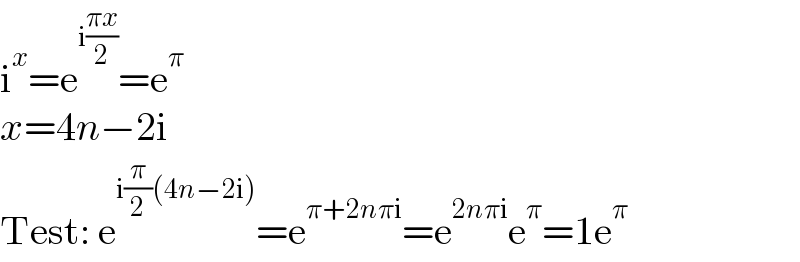
$$\mathrm{i}^{{x}} =\mathrm{e}^{\mathrm{i}\frac{\pi{x}}{\mathrm{2}}} =\mathrm{e}^{\pi} \\ $$$${x}=\mathrm{4}{n}−\mathrm{2i} \\ $$$$\mathrm{Test}:\:\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{n}−\mathrm{2i}\right)} =\mathrm{e}^{\pi+\mathrm{2}{n}\pi\mathrm{i}} =\mathrm{e}^{\mathrm{2}{n}\pi\mathrm{i}} \mathrm{e}^{\pi} =\mathrm{1e}^{\pi} \\ $$
