Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 196429 by SANOGO last updated on 24/Aug/23

Answered by Frix last updated on 24/Aug/23

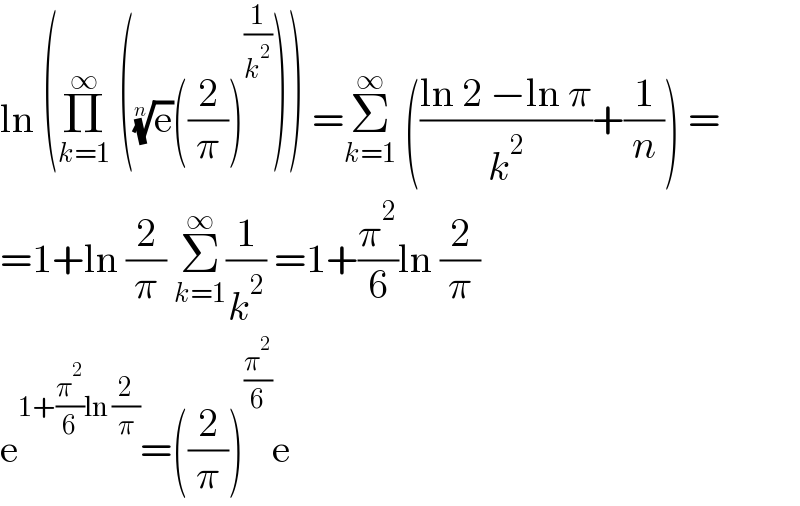
ln (Π_(k=1) ^∞ ((e)^(1/n) ((2/π))^(1/k^2 ) )) =Σ_(k=1) ^∞ (((ln 2 −ln π)/k^2 )+(1/n)) = =1+ln (2/π) Σ_(k=1) ^∞ (1/k^2 ) =1+(π^2 /6)ln (2/π) e^(1+(π^2 /6)ln (2/π)) =((2/π))^(π^2 /6) e

$$\mathrm{ln}\:\left(\underset{{k}=\mathrm{1}} {\overset{\infty} {\prod}}\:\left(\sqrt[{{n}}]{\mathrm{e}}\left(\frac{\mathrm{2}}{\pi}\right)^{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }} \right)\right)\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{ln}\:\mathrm{2}\:−\mathrm{ln}\:\pi}{{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{{n}}\right)\:= \\ $$$$=\mathrm{1}+\mathrm{ln}\:\frac{\mathrm{2}}{\pi}\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\mathrm{ln}\:\frac{\mathrm{2}}{\pi} \\ $$$$\mathrm{e}^{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\mathrm{ln}\:\frac{\mathrm{2}}{\pi}} =\left(\frac{\mathrm{2}}{\pi}\right)^{\frac{\pi^{\mathrm{2}} }{\mathrm{6}}} \mathrm{e} \\ $$

Commented by SANOGO last updated on 24/Aug/23

thank you

$${thank}\:{you} \\ $$

Commented by Frix last updated on 24/Aug/23

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com