
Question Number 196277 by cortano12 last updated on 21/Aug/23

$$\:\:\:\:\:\cancel{\underline{\underbrace{ }}\:} \\ $$
Answered by mr W last updated on 21/Aug/23
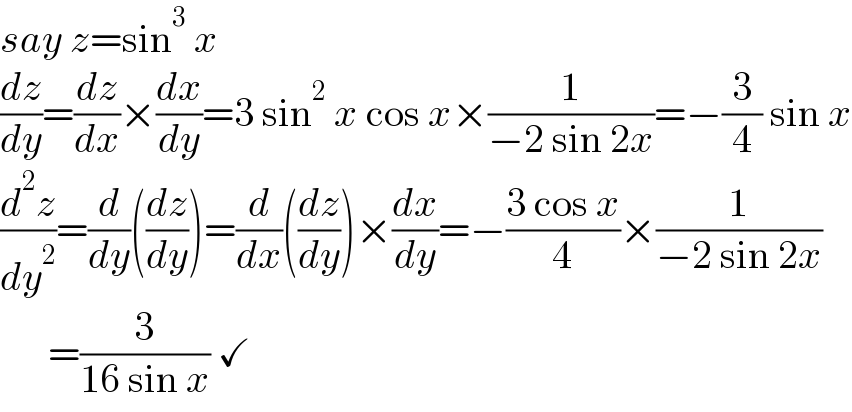
$${say}\:{z}=\mathrm{sin}^{\mathrm{3}} \:{x} \\ $$$$\frac{{dz}}{{dy}}=\frac{{dz}}{{dx}}×\frac{{dx}}{{dy}}=\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}\:{x}×\frac{\mathrm{1}}{−\mathrm{2}\:\mathrm{sin}\:\mathrm{2}{x}}=−\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{sin}\:{x} \\ $$$$\frac{{d}^{\mathrm{2}} {z}}{{dy}^{\mathrm{2}} }=\frac{{d}}{{dy}}\left(\frac{{dz}}{{dy}}\right)=\frac{{d}}{{dx}}\left(\frac{{dz}}{{dy}}\right)×\frac{{dx}}{{dy}}=−\frac{\mathrm{3}\:\mathrm{cos}\:{x}}{\mathrm{4}}×\frac{\mathrm{1}}{−\mathrm{2}\:\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{16}\:\mathrm{sin}\:{x}}\:\checkmark \\ $$
Answered by deleteduser1 last updated on 21/Aug/23
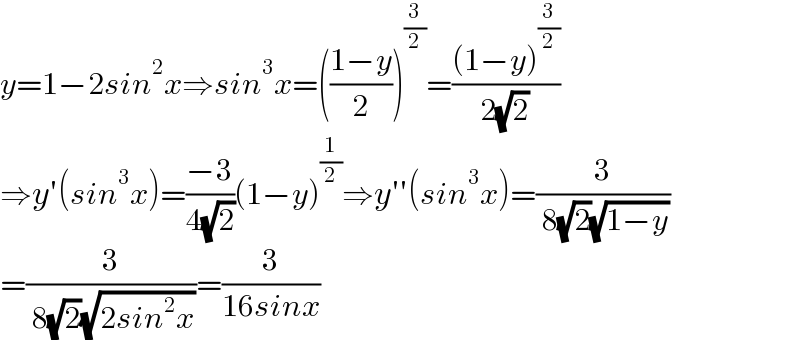
$${y}=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\Rightarrow{sin}^{\mathrm{3}} {x}=\left(\frac{\mathrm{1}−{y}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\left(\mathrm{1}−{y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{y}'\left({sin}^{\mathrm{3}} {x}\right)=\frac{−\mathrm{3}}{\mathrm{4}\sqrt{\mathrm{2}}}\left(\mathrm{1}−{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \Rightarrow{y}''\left({sin}^{\mathrm{3}} {x}\right)=\frac{\mathrm{3}}{\:\mathrm{8}\sqrt{\mathrm{2}}\sqrt{\mathrm{1}−{y}}} \\ $$$$=\frac{\mathrm{3}}{\:\mathrm{8}\sqrt{\mathrm{2}}\sqrt{\mathrm{2}{sin}^{\mathrm{2}} {x}}}=\frac{\mathrm{3}}{\mathrm{16}{sinx}} \\ $$
Answered by horsebrand11 last updated on 22/Aug/23

$$\:\:\:\underline{\underbrace{�}} \\ $$
